题目内容
9．一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有（ ）颗．
| A． | 3 | B． | 5 | C． | 10 | D． | 27 |
分析 由已知可得：相邻两颗白珠之间的黑珠分别为：1，2，3，…，n颗，n∈Z，由盒子遮住前两颗白珠之间有4颗黑珠，盒子遮住后两颗白珠之间有9颗黑珠，进而计算出被盒子遮住的黑珠和白珠的颗数，相加可得答案．
解答 解：由已知可得：相邻两颗白珠之间的黑珠分别为：1，2，3，…，n颗，n∈Z，
由盒子遮住前两颗白珠之间有4颗黑珠，
盒子遮住后两颗白珠之间有9颗黑珠，
故这串珠子被盒子遮住的部分有3颗白珠，
有5+6+7+8-2=24颗黑珠，
故这串珠子被盒子遮住的部分有27颗，
故选：D
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
19．设f（x）=|x2+2x-1|，若a＜b＜-1，且f（a）=f（b），则（a+1）（b+1）的取值范围是（ ）
| A． | （-1，1） | B． | （0，1） | C． | （0，2） | D． | （1，2） |
20．函数f（x）=lnx-x2的极值情况为（ ）
| A． | 无极值 | B． | 有极小值，无极大值 | ||
| C． | 有极大值，无极小值 | D． | 不确定 |
4．甲、乙两人在一次射击测试中各射靶10次，如图分别是这两人命中环数的直方图，若他们的成绩平均数分别为y1和y2，成绩的标准差分别为s1和s2，则（ ）
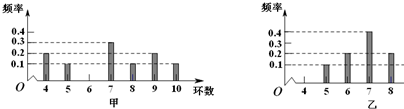
| A． | y1=y2，s1＞s2 | B． | y1=y2，s1＜s2 | C． | y1＞y2，s1=s2 | D． | y1＜y2，s1=s2 |
如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：