题目内容
13.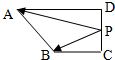 在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].
在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].
分析 根据题意,利用解析法求解,以直线DA,DC分别为x,y轴建立平面直角坐标系,则A(2,0),B(1,1),C(0,1),D(0,0),设P(0,b)(0≤b≤1),求出$\overrightarrow{PA}$,$\overrightarrow{PB}$,根据向量模的计算公式,即可求得,利用完全平方式非负,即可求得其最值.
解答 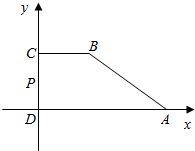 解:如图,以直线DA,DC分别为x,y轴建立平面直角坐标系,
解:如图,以直线DA,DC分别为x,y轴建立平面直角坐标系,
则A(2,0),B(1,1),C(0,1),D(0,0)
设P(0,b)(0≤b≤1)
则$\overrightarrow{PA}$=(2,-b),$\overrightarrow{PB}$=(1,1-b),
∴$\overrightarrow{PA}+3\overrightarrow{PB}$=(5,3-4b)
∴则$|\overrightarrow{PA}+3\overrightarrow{PB}|$=$\sqrt{25+(3-4b)^{2}}$≥5,$|\overrightarrow{PA}+3\overrightarrow{PB}|$=$\sqrt{25+(3-4b)^{2}}$≤$\sqrt{34}$,
故答案为:$[5,\sqrt{34}]$.
点评 此题是个基础题.考查向量在几何中的应用,以及向量模的求法,同时考查学生灵活应用知识分析解决问题的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.等差数列{an}中,首项a1=1,a5=9,则数列的前10项之和是( )
| A. | 90 | B. | 100 | C. | 145 | D. | 190 |
8.全集U={0,1,2,3,5,6,8},集合A={1,5,8},B={2},则集合(∁UA)∪B为( )
| A. | {1,2,5,8} | B. | {0,3,6} | C. | {0,2,3,6} | D. | ∅ |
5.已知函数f(x)=5sin(4x+$\frac{φ}{2}$)(0<φ<2π)为偶函数,则φ等于( )
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |