题目内容
2.已知△ABC的三内角A,B,C满足2B=A+C,则$cos(\frac{π}{3}-A)+cosC$的取值范围为(0,$\sqrt{3}$].分析 由题意可得B=$\frac{π}{3}$,A+C=$\frac{2π}{3}$.利用两角和差的余弦公式化简$cos(\frac{π}{3}-A)+cosC$ 为$\sqrt{3}$sinA,再根据A∈(0,$\frac{2π}{3}$),利用正弦函数的定义域和值域求得 $\sqrt{3}$sinA 的范围.
解答 解:由于△ABC的三内角A,B,C满足2B=A+C,则B=$\frac{π}{3}$,A+C=$\frac{2π}{3}$.
则$cos(\frac{π}{3}-A)+cosC$=cos($\frac{π}{3}$-A)-cos($\frac{π}{3}$+A)=cos$\frac{π}{3}$cosA+sin$\frac{π}{3}$sinA-[cos$\frac{π}{3}$cosA-sin$\frac{π}{3}$sinA]=2sin$\frac{π}{3}$sinA=$\sqrt{3}$sinA,
再根据A∈(0,$\frac{2π}{3}$),可得sinA∈(0,1],∴$\sqrt{3}$sinA∈(0,$\sqrt{3}$],
故答案为:(0,$\sqrt{3}$].
点评 本题主要考查两角和差的余弦公式,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.12,13,16,21,( ),37.
| A. | 25 | B. | 26 | C. | 28 | D. | 31 |
14.已知等差数列中,a4=1,a7+a9=16,则a12的值是( )
| A. | 15 | B. | 30 | C. | 31 | D. | 64 |
12.已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆引切线PQ,且满足|PQ|=|PA|,若以P为圆心所作的圆P与圆O有公共点,则圆P半径的最小值为( )
| A. | $\frac{3\sqrt{5}}{5}$-1 | B. | 1 | C. | 2 | D. | $\frac{3\sqrt{5}}{5}$ |
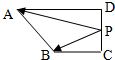 在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].
在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].