题目内容
4.已知a,b∈R+.(1)若loga$\frac{1}{b}$=-2,求证:3a+12b≥9;
(2)若2a+b=1,求ab的最大值.
分析 (1)由题意可得b=$\frac{1}{{a}^{2}}$,可得3a+12b=$\frac{3a}{2}$+$\frac{3a}{2}$+$\frac{12}{{a}^{2}}$由基本不等式可得;
(2)由基本不等式可得ab=$\frac{1}{2}$•2a•b≤$\frac{1}{2}$($\frac{2a+b}{2}$)2=$\frac{1}{8}$,验证等号成立即可.
解答 解:(1)∵loga$\frac{1}{b}$=-2,∴$\frac{1}{b}$=a2,∴b=$\frac{1}{{a}^{2}}$,
∴3a+12b=3a+$\frac{12}{{a}^{2}}$=$\frac{3a}{2}$+$\frac{3a}{2}$+$\frac{12}{{a}^{2}}$≥3$\root{3}{\frac{3a}{2}•\frac{3a}{2}•\frac{12}{{a}^{2}}}$=9
当且仅当$\frac{3a}{2}$=$\frac{12}{{a}^{2}}$即a=2且b=$\frac{1}{4}$时取等号,
∴3a+12b≥9;
(2)∵正数ab满足2a+b=1,
∴ab=$\frac{1}{2}$•2a•b≤$\frac{1}{2}$($\frac{2a+b}{2}$)2=$\frac{1}{8}$,
当且仅当2a=b即a=$\frac{1}{4}$且b=$\frac{1}{2}$时取等号,
∴ab的最大值为$\frac{1}{8}$
点评 本题考查不等式的证明,涉及基本不等式求最值,属中档题.

练习册系列答案
相关题目
14.集合M={m|m=2n-1,n∈N*,m<60}的元素个数是( )
| A. | 59 | B. | 31 | C. | 30 | D. | 29 |
15.已知实数a,b,c满足b+c=3a2-4a+6,c-b=a2-4a+4,则a,b,c的大小关系是( )
| A. | c≥b>a | B. | c>b>a | C. | a>c≥b | D. | a>c>b |
14.已知等差数列中,a4=1,a7+a9=16,则a12的值是( )
| A. | 15 | B. | 30 | C. | 31 | D. | 64 |
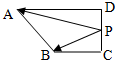 在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].
在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].