题目内容
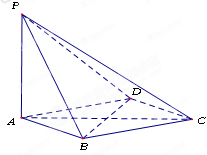
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=,PA=,∠ABC=120°,G为线段PC的中点.

(1)证明:PA//平面BGD;
(2)求直线DG与平面PAC所成的角的正切值.

(1)证明:PA//平面BGD;
(2)求直线DG与平面PAC所成的角的正切值.
(1)见解析(2)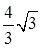
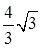
试题分析:(1) 求证线面平行就要找够平行条件,平面
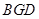 外直线
外直线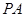 ,差平面内直线,在四棱锥中找过
,差平面内直线,在四棱锥中找过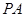 的平面
的平面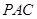 与平面
与平面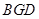 相交
相交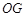 ,再证明交线
,再证明交线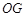 与
与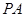 平行;
平行;(2)由三角形的中位线性质以及条件证明∠DGO为DG与平面PAC所成的角,求出GO和AC的值,可得OC、OD的值,再利用直角三角形中的边角关系求得tan∠DGO的值.
试题解析:
(1)证明:设点O为AC、BD的交点,由AB=BC,AD=CD,得BD是线段AC的中垂线,所以O为AC的中点, 连结OG又因为G为PC的中点,所以
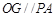 (3分)
(3分)又因为
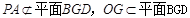 所以PA//面BGD (6分)
所以PA//面BGD (6分)(2)
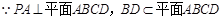
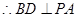 ,又由(1)知
,又由(1)知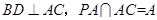
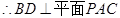 ,所以
,所以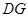 与面
与面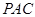 所成的角是
所成的角是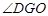 .(8分)
.(8分)由 (1)知:
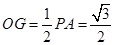 ,
,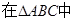
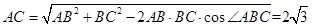 ,所以
,所以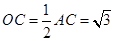
在直角
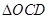 中,
中,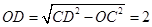
在直角
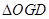 中,
中, 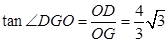 ,
,所以直线
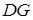 与面
与面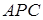 所成的角的正切值是
所成的角的正切值是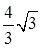 . (12分)
. (12分)
练习册系列答案
相关题目
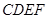 为正方形,平面
为正方形,平面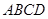 为等腰梯形,
为等腰梯形,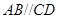 ,
,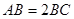 ,
,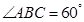 ,
, .
.
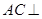 平面
平面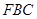 ;
;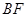 与平面
与平面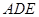 所成角的正弦值.
所成角的正弦值. 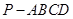 中,
中,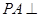 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,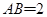 ,
,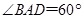 .
.
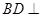 平面PAC;
平面PAC;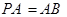 ,求
,求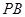 与
与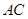 所成角的余弦值;
所成角的余弦值; 中,底面
中,底面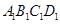 是正方形,
是正方形,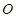 是
是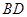 的中点,
的中点,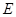 是棱
是棱 上任意一点.
上任意一点.
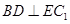 ;
;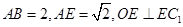 ,求
,求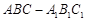 中,
中,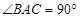 ,
,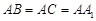 ,且
,且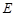 是
是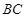 中点.
中点.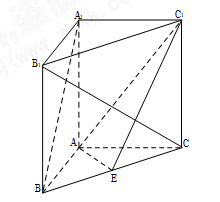
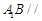 平面
平面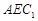 ;
;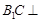 平面
平面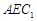 .
.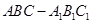 中,D、E分别为
中,D、E分别为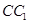 、AD的中点,F为
、AD的中点,F为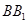 上的点,且
上的点,且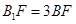
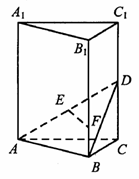
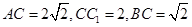 ,
,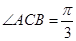 ,求二面角
,求二面角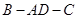 的大小.
的大小.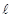 ⊥平面
⊥平面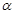 ,直线m
,直线m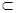 平面
平面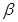 ,有下面四个命题:
,有下面四个命题: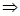
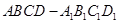 中,点
中,点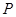 在侧面
在侧面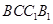 及其边界上运动,并且总是保持
及其边界上运动,并且总是保持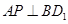 ,则动点
,则动点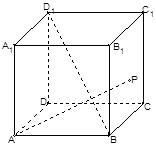
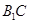
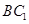
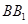 中点与
中点与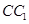 中点连成的线段
中点连成的线段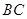 中点与
中点与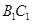 中点连成的线段
中点连成的线段