题目内容
已知直线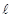 ⊥平面
⊥平面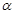 ,直线m
,直线m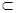 平面
平面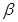 ,有下面四个命题:
,有下面四个命题:
①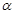 ∥
∥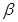
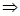
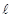 ⊥m;②
⊥m;②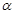 ⊥
⊥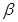
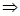
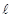 ∥m;③
∥m;③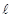 ∥m
∥m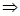
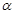 ⊥
⊥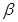 ;④
;④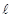 ⊥m
⊥m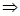
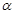 ∥
∥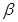
其中正确命题序号是 .
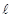 ⊥平面
⊥平面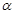 ,直线m
,直线m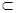 平面
平面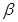 ,有下面四个命题:
,有下面四个命题:①
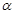 ∥
∥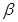
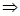
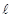 ⊥m;②
⊥m;②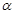 ⊥
⊥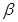
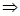
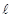 ∥m;③
∥m;③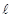 ∥m
∥m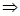
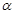 ⊥
⊥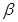 ;④
;④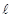 ⊥m
⊥m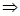
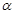 ∥
∥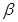
其中正确命题序号是 .
①③
试题分析:本题考查直线与平面垂直的判定与性质,直线
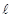 ⊥平面
⊥平面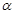 ,
,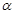 ∥
∥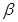
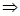
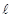 ⊥
⊥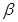
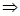
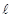 ⊥m,①对;
⊥m,①对;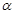 ⊥
⊥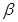 ,
,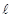 ⊥
⊥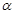 时直线
时直线 与平面
与平面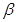 可能平行,也可能线在面内,直线
可能平行,也可能线在面内,直线 与直线
与直线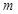 关系不确定,②错;
关系不确定,②错;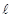 ∥m,
∥m,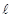 ⊥
⊥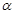 ,
,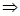 m⊥
m⊥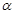
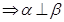 ,③对;由
,③对;由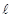 ⊥m,不能得出
⊥m,不能得出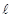 ⊥
⊥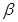 ,故也不能有
,故也不能有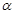 ∥
∥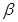 ,④错.
,④错.
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目

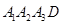 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.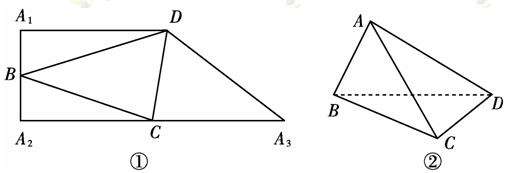
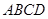 的体积。
的体积。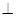 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN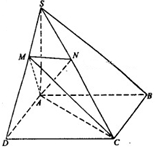
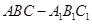 是一个斜三棱柱,已知
是一个斜三棱柱,已知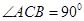 、平面
、平面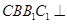 平面
平面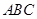 、
、 、
、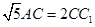 ,又
,又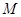 、
、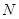 分别是
分别是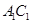 、
、 的中点.
的中点.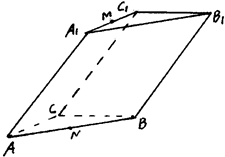
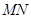 ∥平面
∥平面 ; (2)求二面角
; (2)求二面角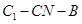 的大小.
的大小.
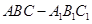 中,侧面
中,侧面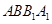 ,
,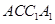 均为正方形,∠
均为正方形,∠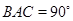 ,点
,点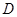 是棱
是棱 的中点.
的中点.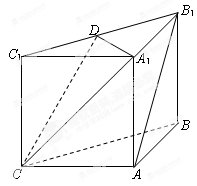
 ⊥平面
⊥平面 ;
;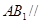 平面
平面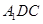 ;
;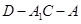 的余弦值.
的余弦值.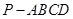 中,底面
中,底面 为菱形,
为菱形,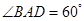 ,
,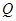 为
为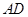 的中点.
的中点.
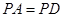 ,求证:平面
,求证:平面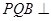 平面
平面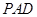 ;
; 在线段
在线段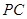 上,
上,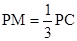 ,若平面
,若平面 平面
平面 ,且
,且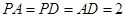 ,求二面角
,求二面角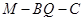 的大小.
的大小.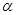 不垂直平面
不垂直平面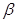 ,那么平面
,那么平面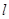 不平行平面
不平行平面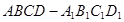 中,
中,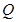 是
是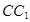 的中点,
的中点,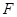 是侧面
是侧面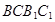 内的动点且
内的动点且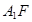 //平面
//平面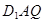 ,则
,则