题目内容
如图,在四棱锥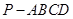 中,
中,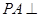 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,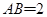 ,
,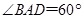 .
.
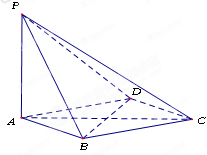
(1)求证: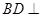 平面PAC;
平面PAC;
(2)若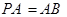 ,求
,求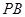 与
与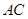 所成角的余弦值;
所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
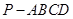 中,
中,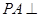 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,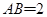 ,
,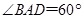 .
.
(1)求证:
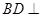 平面PAC;
平面PAC;(2)若
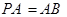 ,求
,求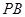 与
与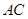 所成角的余弦值;
所成角的余弦值;(3)当平面PBC与平面PDC垂直时,求PA的长.
(1)证明见解析;(2)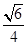 ;(3)
;(3)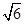 .
.
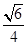 ;(3)
;(3)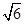 .
.试题分析:(1)要证线面垂直,就是要证这条直线与平面内的两条相交直线垂直,这里由于四边形
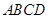 是菱形,所以
是菱形,所以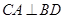 ,另外一条直线当然考虑
,另外一条直线当然考虑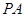 (或者
(或者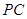 ),本题中应该是
),本题中应该是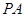 ;(2)求异面直线所成的角,一般可通过平移变成相交直线所成的角,考虑到第(3)小题问题,且题中有垂直的直线,故考虑建立空间直角坐标系(以
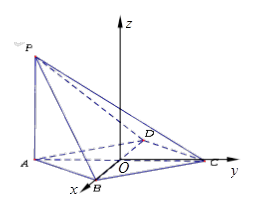
;(2)求异面直线所成的角,一般可通过平移变成相交直线所成的角,考虑到第(3)小题问题,且题中有垂直的直线,故考虑建立空间直角坐标系(以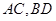 的交点
的交点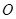 为坐标原点,
为坐标原点,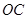 为
为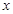 轴,
轴,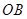 为
为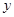 轴,过
轴,过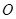 与
与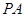 平行的直线为
平行的直线为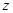 轴),则
轴),则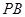 与
与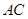 所成角就是
所成角就是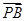 与
与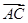 的夹角((锐角(或其补角)或直角),平面
的夹角((锐角(或其补角)或直角),平面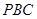 与平面
与平面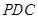 垂直就是它们的法向量垂直,即它们的法向量的数量积为0.
垂直就是它们的法向量垂直,即它们的法向量的数量积为0.试题解析:(1)证明:因为四边形
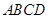 是菱形,所以
是菱形,所以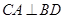 ,又因为
,又因为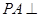 平面
平面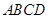 ,所以
,所以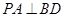 ,而
,而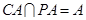 ,所以
,所以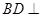 平面
平面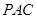 .
.
(2)设
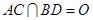 ,因为
,因为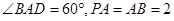 ,
,所以
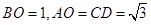 ,如图,以
,如图,以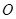 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系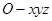 ,则
,则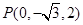 ,
,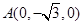 ,
,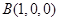 ,
,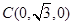 ,
,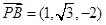 ,
,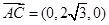 ,设
,设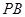 与
与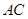 所成的角为
所成的角为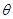 ,则
,则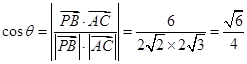 .
.(3)由(2)知
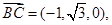 设
设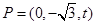
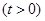 .则
.则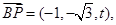 设平面
设平面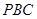 的法
的法向量
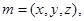 则
则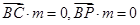 ,所以
,所以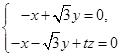 令
令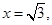 则
则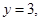
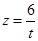 ,
,所以
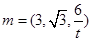 同理,平面
同理,平面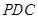 的法向量
的法向量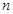
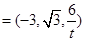 ,因为平面
,因为平面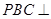
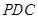 ,所以
,所以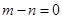 ,即
,即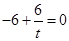 解得
解得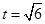 ,所以
,所以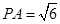 .
.
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
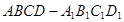 中,
中,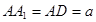 ,
,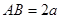 , E、
, E、 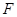 分别为
分别为 、
、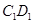 的中点.
的中点.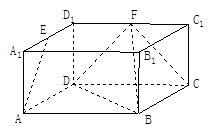
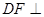 平面
平面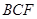 ;
;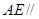 平面
平面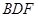 .
. 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN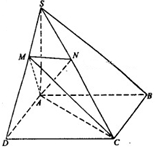
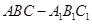 是一个斜三棱柱,已知
是一个斜三棱柱,已知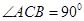 、平面
、平面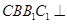 平面
平面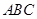 、
、 、
、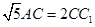 ,又
,又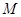 、
、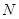 分别是
分别是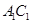 、
、 的中点.
的中点.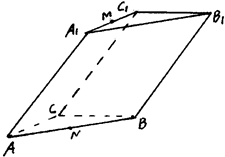
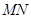 ∥平面
∥平面 ; (2)求二面角
; (2)求二面角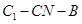 的大小.
的大小.
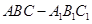 中,侧面
中,侧面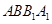 ,
,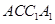 均为正方形,∠
均为正方形,∠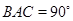 ,点
,点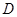 是棱
是棱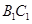 的中点.
的中点.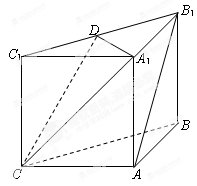
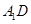 ⊥平面
⊥平面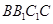 ;
;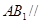 平面
平面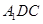 ;
;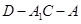 的余弦值.
的余弦值.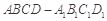 ,中,
,中,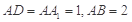 ,点
,点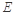 在棱AB上移动.
在棱AB上移动.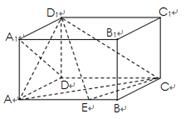
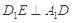 ;
; 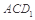 的距离;
的距离;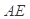 等于何值时,二面角
等于何值时,二面角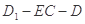 的大小为
的大小为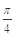
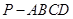 中,底面
中,底面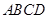 是边长为
是边长为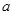 的正方形,侧面
的正方形,侧面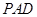
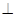 底面
底面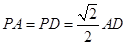 ,设
,设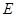 、
、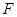 分别为
分别为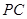 、
、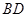 的中点.
的中点.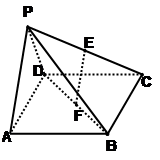
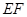 //平面
//平面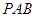
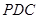 .
.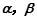 和两条不同直线
和两条不同直线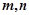 ,则下列说法正确的是( )
,则下列说法正确的是( )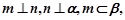 则
则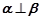
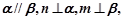 则
则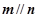
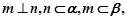 则
则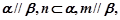 则
则