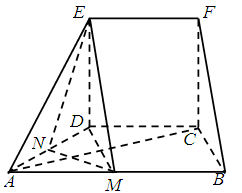
题目内容
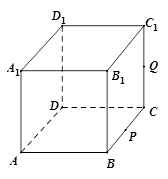
在如图的几何体中,平面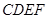 为正方形,平面
为正方形,平面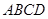 为等腰梯形,
为等腰梯形,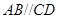 ,
,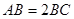 ,
,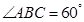 ,
, .
.

(1)求证: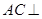 平面
平面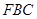 ;
;
(2)求直线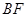 与平面
与平面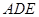 所成角的正弦值.
所成角的正弦值.
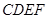 为正方形,平面
为正方形,平面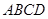 为等腰梯形,
为等腰梯形,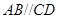 ,
,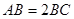 ,
,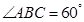 ,
, .
.
(1)求证:
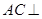 平面
平面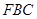 ;
;(2)求直线
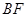 与平面
与平面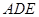 所成角的正弦值.
所成角的正弦值. (1)详见解析;(2) .
.
 .
.试题分析:(1)先利用余弦定理以及
 得到
得到 与
与 的等量关系,然后利用勾股定理证明
的等量关系,然后利用勾股定理证明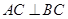 ,再结合已知条件
,再结合已知条件 并利用直线与平面垂直的判定定理证明
并利用直线与平面垂直的判定定理证明 平面
平面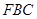 ;证法二是在
;证法二是在 中利用正弦定理并结合三角函数求出
中利用正弦定理并结合三角函数求出 的大小,进而得到
的大小,进而得到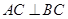 ,再结合已知条件
,再结合已知条件 并利用直线与平面垂直的判定定理证明
并利用直线与平面垂直的判定定理证明 平面
平面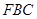 ;(2)解法一是将
;(2)解法一是将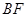 进行平移使得与平面
进行平移使得与平面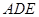 相交,即取
相交,即取 的中点
的中点 ,通过证明四边形
,通过证明四边形 为平行四边形来达到证明
为平行四边形来达到证明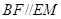 的目的,于是将问题转化为求直线
的目的,于是将问题转化为求直线 与平面
与平面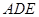 的角的正弦值,取
的角的正弦值,取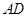 的中点
的中点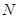 ,先证明
,先证明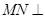 平面
平面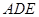 ,于是得到直线
,于是得到直线 与平面
与平面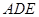 所成的角为
所成的角为 ,最后在直角三角形
,最后在直角三角形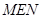 中计算
中计算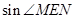 的值;解法二是建立以点
的值;解法二是建立以点 为坐标原点,
为坐标原点, 、
、 、
、 所在的直线分别为
所在的直线分别为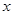 轴、
轴、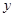 轴、
轴、 轴的空间直角坐标系,利用空间向量法求直线
轴的空间直角坐标系,利用空间向量法求直线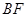 与平面
与平面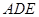 所成角的正弦值.
所成角的正弦值.试题解析:(1)证明1:因为
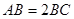 ,
,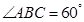 ,
,在
 中,由余弦定理可得
中,由余弦定理可得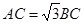 ,
,以
 .所以
.所以 ,
,因为
 ,
,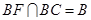 ,
,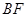 、
、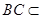 平面
平面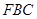 ,
,所以
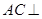 平面
平面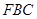 .
. 证明2:因为
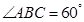 ,设
,设
 ,则
,则 ,
,在△
 中,由正弦定理,得
中,由正弦定理,得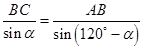 .
.为
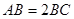 ,所以
,所以 .
.整理得
 ,所以
,所以 .所以
.所以 .
.因为
 ,
,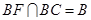 ,
,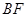 、
、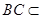 平面
平面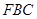 ,
,所以
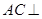 平面
平面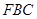 ;
; (2)解法1:由(1)知,
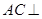 平面
平面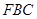 ,
,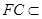 平面
平面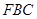 ,
,所以
 .
.因为平面
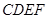 为正方形,所以
为正方形,所以 .
.因为
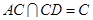 ,所以
,所以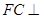 平面
平面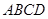 ,
, 取
 的中点
的中点 ,连结
,连结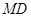 ,
, ,
,因为
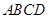 是等腰梯形,且
是等腰梯形,且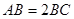 ,
, ,
,所以
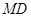
 .所以
.所以 是等边三角形,且
是等边三角形,且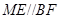 ,
,
取
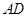 的中点
的中点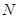 ,连结
,连结 、
、 ,则
,则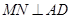 .
.因为
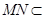 平面
平面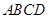 ,
,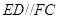 ,所以
,所以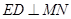 ,
,因为
 ,所以
,所以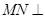 平面
平面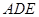 ,
,所以
 为直线
为直线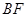 与平面
与平面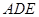 所成角,
所成角,因为
 平面
平面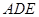 ,所以
,所以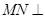
 ,
,因为
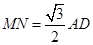 ,
, ,
,在
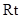 △
△ 中,
中, .所以直线
.所以直线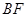 与平面
与平面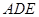 所成角的正弦值为
所成角的正弦值为 ;
;解法2:由(1)知,
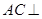 平面
平面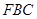 ,
,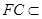 平面
平面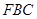 ,
,所以
 .
.因为平面
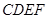 为正方形,所以
为正方形,所以 .
.因为
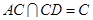 ,所以
,所以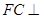 平面
平面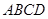 ,所以
,所以 、
、 、
、 两两互相垂直.
两两互相垂直.建立如图的空间直角坐标系
 ,
,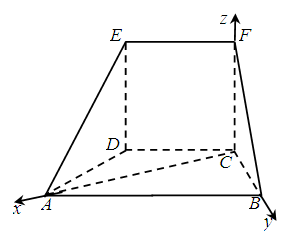
因为
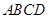 是等腰梯形,且
是等腰梯形,且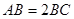 ,
,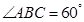
所以
 .
.不妨设
 ,则
,则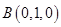 ,
,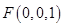 ,
, ,
,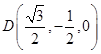 ,
,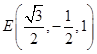 ,
,所以
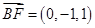 ,
,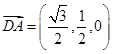 ,
, .
.设平面
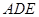 的法向量为
的法向量为 ,则有
,则有 ,即
,即 ,
,取
 ,得
,得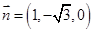 是平面
是平面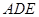 的一个法向量,
的一个法向量,设直线
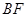 与平面
与平面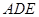 所成的角为
所成的角为 ,
,则
 ,
,所以直线
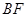 与平面
与平面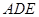 所成角的正弦值为
所成角的正弦值为 .
.
练习册系列答案
相关题目
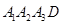 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.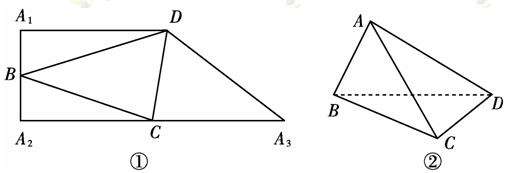
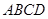 的体积。
的体积。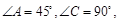
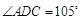 ,
,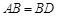 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD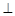 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

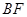 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 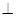 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN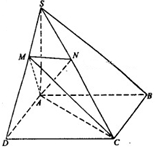

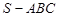 中,侧面
中,侧面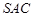 与底面
与底面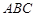 垂直,
垂直, 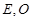 分别是
分别是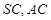 的中点,
的中点,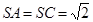
 ,
,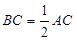 ,
, .
.
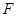 在线段
在线段 上,问:无论
上,问:无论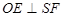 ?请证明你的结论;
?请证明你的结论;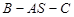 的平面角的余弦.
的平面角的余弦.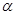 、
、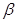 是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是
是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是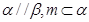 ,则
,则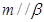
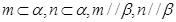 ,则
,则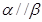
 ,则
,则
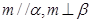 ,则
,则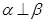
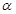 外不共线的三点
外不共线的三点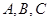 到
到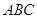 必平行于
必平行于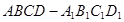 中,
中,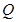 是
是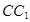 的中点,
的中点,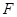 是侧面
是侧面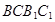 内的动点且
内的动点且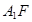 //平面
//平面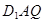 ,则
,则