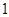题目内容
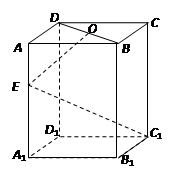
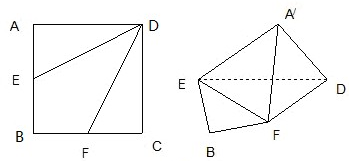
如图长方体 中,底面
中,底面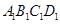 是正方形,
是正方形, 是
是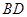 的中点,
的中点,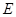 是棱
是棱 上任意一点.
上任意一点.
⑴求证: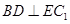 ;
;
⑵如果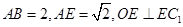 ,求
,求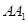 的长.
的长.
 中,底面
中,底面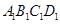 是正方形,
是正方形,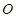 是
是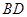 的中点,
的中点,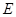 是棱
是棱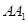 上任意一点.
上任意一点.
⑴求证:
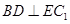 ;
;⑵如果
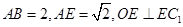 ,求
,求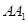 的长.
的长.(1)证明见解析;(2)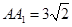 .
.
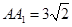 .
.试题分析:(1)要证线线垂直,一般可先证线面垂直,这个平面要包含其中一条直线,本题中有许多垂直关系,如
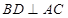 ,而
,而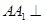 平面
平面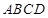
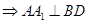 ,因此有
,因此有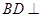 平面
平面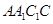 ,
,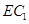 正好是平面
正好是平面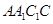 内的直线,问题得证;(2)我们采取空间问题平面化,所有条件都可在矩形
内的直线,问题得证;(2)我们采取空间问题平面化,所有条件都可在矩形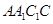 内,利用平面几何知识解题,由于
内,利用平面几何知识解题,由于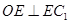 ,则有
,则有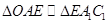 ,这两个三角形中,有
,这两个三角形中,有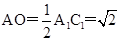 ,又
,又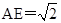 ,这时可求出
,这时可求出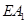 ,从而求出
,从而求出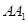 的长.
的长.试题解析:(1)
 是正方形,∴
是正方形,∴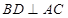 ,又长方体的侧棱
,又长方体的侧棱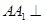 平面
平面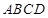 ,∴
,∴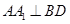 ,
,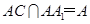 ,故有
,故有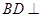 平面
平面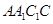 ,又
,又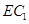
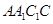 ,∴
,∴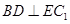 . 7分
. 7分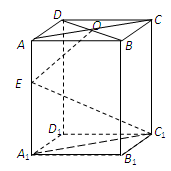
(2)在长方体
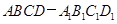 中,
中,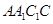 是矩形,由
是矩形,由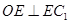 ,得
,得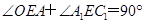 ,∴
,∴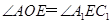 ,从而
,从而 ,∴
,∴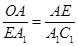 ,又底面正方形
,又底面正方形 的边长为2,故
的边长为2,故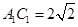 ,
,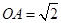 ,又
,又 ,∴
,∴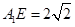 ,从而
,从而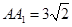 . 14分
. 14分说明:用空间向量知识求解相应给分.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 中,侧面
中,侧面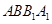 ,
,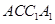 均为正方形,∠
均为正方形,∠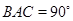 ,点
,点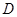 是棱
是棱 的中点.
的中点.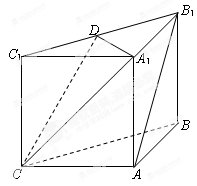
 ⊥平面
⊥平面 ;
;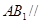 平面
平面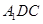 ;
;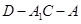 的余弦值.
的余弦值. ,底面
,底面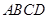 是平行四边形,点
是平行四边形,点 在平面
在平面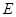 在
在 边上,且
边上,且 ,
,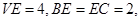
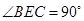 .
.
 是
是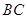 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值; 在棱
在棱 .求
.求 的值.
的值.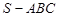 中,侧面
中,侧面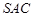 与底面
与底面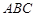 垂直,
垂直,  分别是
分别是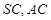 的中点,
的中点,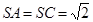
 ,
,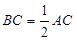 ,
, .
.
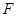 在线段
在线段 上,问:无论
上,问:无论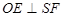 ?请证明你的结论;
?请证明你的结论;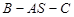 的平面角的余弦.
的平面角的余弦.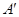
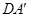 ⊥EF;
⊥EF;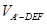
 外不共线的三点
外不共线的三点 到
到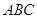 必平行于
必平行于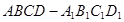 中,
中, 是
是 的中点,
的中点,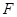 是侧面
是侧面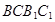 内的动点且
内的动点且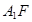 //平面
//平面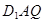 ,则
,则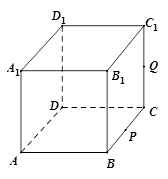
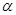 、
、 是两个不同的平面,
是两个不同的平面,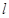 是一条直线,以下命题:
是一条直线,以下命题: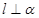 ,
,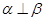 ,则
,则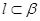 ;②若
;②若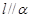 ,
,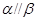 ,则
,则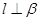 ;④若
;④若