题目内容
【题目】设椭圆E: ![]() +y2=1(a>1)的右焦点为F,右顶点为A,已知
+y2=1(a>1)的右焦点为F,右顶点为A,已知 ![]() ,其中O为原点,e为椭圆的离心率.
,其中O为原点,e为椭圆的离心率.
(Ⅰ)求a的值;
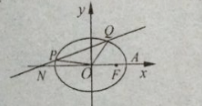
(Ⅱ)动直线l过点N(﹣2,0),l与椭圆E交于P,Q两点,求△OPQ面积的最大值.
【答案】解:(Ⅰ)由椭圆E: ![]() +y2=1(a>1)的右焦点为F,b=1,由椭圆的几何性质可知:丨FA丨=a﹣c,丨OF丨=c,丨OA丨=a,
+y2=1(a>1)的右焦点为F,b=1,由椭圆的几何性质可知:丨FA丨=a﹣c,丨OF丨=c,丨OA丨=a,
由 ![]() ,整理得(a﹣c)(
,整理得(a﹣c)( ![]() )=
)= ![]() ,整理得:a2=2c2 ,
,整理得:a2=2c2 ,
由a2﹣c2=b2=1,解得:c=1,则a= ![]() ,
,
∴a的值 ![]() ;
;
(Ⅱ)由(Ⅰ)可知:椭圆的标准方程为: ![]() ,
,
由题l与x轴不重合,设l的方程是x=my﹣2,
由 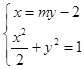 ,整理得(my﹣2)2+2y2﹣2=0,
,整理得(my﹣2)2+2y2﹣2=0,
即(m2+2)y2﹣4my+2=0,
∵直线与椭圆有相异交点,
△=16m2﹣8(m2+2)>0,解得m> ![]() 或m<﹣
或m<﹣ ![]() ,
,
由韦达定理可知:y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,
,
由△OPQ面积S= ![]() 丨ON丨丨y1﹣y2丨=
丨ON丨丨y1﹣y2丨= ![]() 丨ON丨
丨ON丨 ![]() =
= ![]() ,
,
令t= ![]() >0,
>0,
则S= ![]() =
= ![]() ≤
≤ 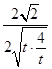 =
= ![]() .
.
当且仅当t=2,即m=± ![]() 时,△OPQ面积的最大,最大值是
时,△OPQ面积的最大,最大值是 ![]() .
.
【解析】(Ⅰ)由椭圆的性质可知:丨FA丨=a﹣c,丨OF丨=c,丨OA丨=a,代入 ![]() ,求得a2=2c2 , 由a2﹣c2=b2=1,即可求得a=
,求得a2=2c2 , 由a2﹣c2=b2=1,即可求得a= ![]() ;(Ⅱ)由题意可知:设l的方程是x=my﹣2,代入椭圆方程,由△>0求得m的取值范围,根据韦达定理及三角形的面积公式S=
;(Ⅱ)由题意可知:设l的方程是x=my﹣2,代入椭圆方程,由△>0求得m的取值范围,根据韦达定理及三角形的面积公式S= ![]() 丨ON丨
丨ON丨 ![]() =
= ![]() ,令t=
,令t= ![]() >0,则S=
>0,则S= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() ,即可求得m的最大值.
,即可求得m的最大值.

练习册系列答案
相关题目