题目内容
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
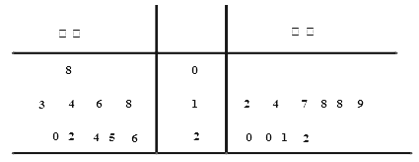
规定:当产品中的此种元素含量![]() 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)甲厂优等品率为![]() , 乙厂优等品率为
, 乙厂优等品率为![]() .
.
(2)![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
故的数学期望为![]()
【解析】
试题(1)因为通过阅读茎叶图可得到甲、乙两组测量值的数据,又因为当产品中的此种元素含量![]() 毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
(2)因为从乙地抽出的上述10件产品中,随机抽取3件,由于乙产品中优质品有8件,所以优质品的件数共有三种情况,通过计算每种情况的概率以及数学期望的计算公式即可得到结论.
试题解析:(I)甲厂抽取的样本中优等品有7件,优等品率为![]()
乙厂抽取的样本中优等品有8件,优等品率为![]()
(II)![]() 的取值为1,2,3.
的取值为1,2,3.
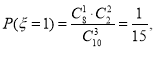
![]()
![]()
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
故的数学期望为![]()

 阅读快车系列答案
阅读快车系列答案【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
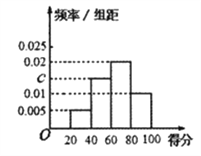
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
