题目内容
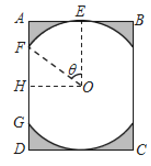
【题目】如图,某城市小区有一个矩形休闲广场,![]() 米,广场的一角是半径为
米,广场的一角是半径为![]() 米的扇形
米的扇形![]() 绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅
绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅![]() (宽度不计),点
(宽度不计),点![]() 在线段
在线段![]() 上,并且与曲线
上,并且与曲线![]() 相切;另一排为单人弧形椅沿曲线
相切;另一排为单人弧形椅沿曲线![]() (宽度不计)摆放.已知双人靠背直排椅的造价每米为
(宽度不计)摆放.已知双人靠背直排椅的造价每米为![]() 元,单人弧形椅的造价每米为
元,单人弧形椅的造价每米为![]() 元,记锐角
元,记锐角![]() ,总造价为
,总造价为![]() 元.
元.
(1)试将![]() 表示为
表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)如何选取点![]() 的位置,能使总造价
的位置,能使总造价![]() 最小.
最小.
【答案】(1)![]()
![]() (2)
(2)![]()
【解析】
试题分析:(1)总造价由两部分组成,根据弧长公式可求得![]() ,而切线长
,而切线长![]() 需构造直角三角形或借助坐标求解,最后由线段长为正,可得
需构造直角三角形或借助坐标求解,最后由线段长为正,可得![]() 的取值范围(2)利用导数求函数最值,先求导数,确定导函数零点,列表分析函数单调性变化趋势,确定极值点,即最值点.
的取值范围(2)利用导数求函数最值,先求导数,确定导函数零点,列表分析函数单调性变化趋势,确定极值点,即最值点.
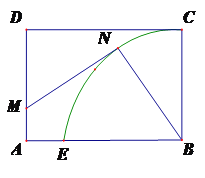
试题解析:解:(1)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ;过
;过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
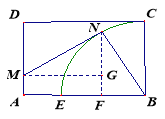
在![]() 中,
中,![]() ,则
,则![]()
在![]() 中,
中,![]() ,
,
由题意易得![]()
因此,![]()
![]()
(2)![]()
令![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
设锐角![]() 满足
满足![]() ,
, ![]()
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当![]() ,总造价
,总造价![]() 最小,最小值为
最小,最小值为![]() ,此时
,此时![]() ,
,![]() ,
,![]() ,因此当
,因此当![]() 米时,能使总造价最小.
米时,能使总造价最小.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
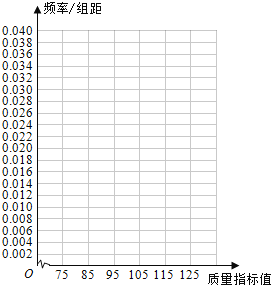
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
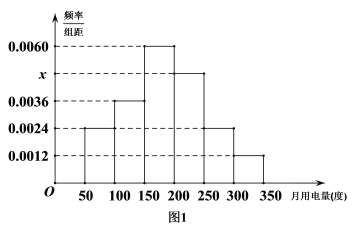
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图1.
A类用户 | B类用户 | |||||||
9 | 7 | 7 | 0 | 6 | ||||
8 | 6 | 5 | 1 | 7 | 8 | 9 | ||
9 | 8 | 2 | 8 | 5 | 6 | 7 | 8 | |
8 | 7 | 1 | 0 | 9 | 7 | 8 | 9 | |
图2
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;(2)若将用电量在区间
的值并估计这50户用户的平均用电量;(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
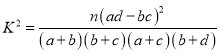 ,
,![]() .
.