Question

【题目】已知函数f（x）= 的定义域为（﹣1，1），满足f（﹣x）=﹣f（x），且f（ ）= ．
（1）求函数f（x）的解析式；
（2）证明f（x）在（﹣1，1）上是增函数；
（3）解不等式f（x2﹣1）+f（x）＜0．

Answer 1

【答案】
（1）解：由题意知，f（x）为奇函数；

∴f（0）=b=0，则 ；

又 ；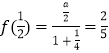

∴a=1；

∴ ；

（2）解：设﹣1＜x1＜x2＜1，则：

= ；

又﹣1＜x1＜x2＜1；

∴ ；

∴f（x1）﹣f（x2）＜0；

即f（x1）＜f（x2）；

∴f（x）在（﹣1，1）上是增函数

（3）解：由f（x2﹣1）+f（x）＜0得f（x2﹣1）＜﹣f（x）；

即f（x2﹣1）＜f（﹣x）；

由（2）知f（x）在（﹣1，1）上是增函数，则 ；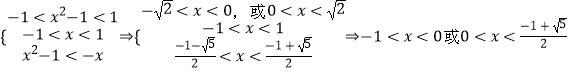

∴原不等式的解集为 ．

【解析】1、利用函数为奇函数，则有f（0）=b=0成立，即得b=0。再根据f（ ）= 得a=1即得函数的解析式。
2、利用定义证明函数的增减性。
3、由题意可得f（x2﹣1）＜f（﹣x），再根据函数的增减性可得, 不等式求交集即可得到结果。

【考点精析】通过灵活运用函数单调性的判断方法和函数单调性的性质，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集即可以解答此题．