题目内容
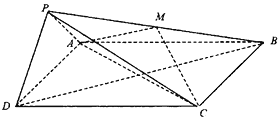
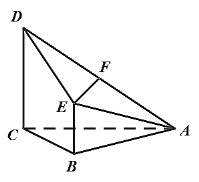
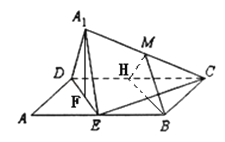
【题目】如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△![]() DE,使平面
DE,使平面![]() DE⊥平面BCDE,若M为线段
DE⊥平面BCDE,若M为线段![]() C的中点,下面四个命题中不正确的是( )
C的中点,下面四个命题中不正确的是( )
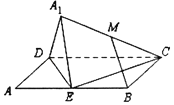
A.BM![]() 平面
平面![]() DEB.CE⊥平面
DEB.CE⊥平面![]() DE
DE
C.DE![]() BMD.平面
BMD.平面![]() CD⊥平面
CD⊥平面![]() CE
CE
【答案】C
【解析】
取CD中点H,DE中点F,连接MH,BH,![]() ,根据线面平行判定定理,线面垂直判定定理和面面垂直判定定理,逐一分析选项,即得。
,根据线面平行判定定理,线面垂直判定定理和面面垂直判定定理,逐一分析选项,即得。
取CD中点H,连接MH,BH,![]() M和H分别是
M和H分别是![]() ,CD的中点,
,CD的中点,![]() ,
,![]() 在平面
在平面![]() 外,
外,![]() 平面
平面![]() ,
,![]() E是矩形ABCD的AB边中点,
E是矩形ABCD的AB边中点,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 在平面
在平面![]() 外,
外,![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,A正确;取DE中点F,连接
,A正确;取DE中点F,连接![]() ,
,![]() 点是矩形ABCD的中点,AB=2AD=2,
点是矩形ABCD的中点,AB=2AD=2,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() 平面BCDE,且DE为两平面交线,
平面BCDE,且DE为两平面交线,![]() 平面BCDE,
平面BCDE,![]() ,
,![]() 平面
平面![]() ,B正确;由选项A可知,
,B正确;由选项A可知,![]() ,HB交MB于点B,故DE与BM不平行,C不正确;由选项B可知,
,HB交MB于点B,故DE与BM不平行,C不正确;由选项B可知,![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,D正确.
,D正确.
故选:C

【题目】“读书可以让人保持思想活跃,让人得到智慧启发,让人滋养浩然之气”,2018年第一期中国青年阅读指数数据显示,从供给的角度,文学阅读域是最多的,远远超过了其他阅读域的供给量.某校采用分层抽样的方法从1000名文科生和2000名理科生中抽取300名学生进行了在暑假阅读内容和阅读时间方面的调查,得到数据如表:
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 130 | ||
文科生 | 45 | ||
合计 |
(1)先完成上面的表格,并判断能否有90%的把握认为学生所学文理与阅读内容有关?
(2从300名被调查的学生中,随机进取30名学生,整理其日平均阅读时间(单位:分钟)如表:
阅读时间 |
|
|
|
|
|
男生人数 | 2 | 4 | 3 | 5 | 2 |
女生人数 | 1 | 3 | 4 | 3 | 3 |
试估计这30名学生日阅读时间的平均值(同一组中的数据以这组数据所在区间中点的值作代表)
(3)从(2)中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得,求这两人都是女生的概率.
参考公式: 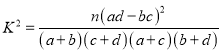 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |