题目内容
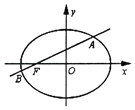
【题目】设椭圆方程
（
），
，
是椭圆的左右焦点，以，及椭圆短轴的一个端点为顶点的三角形是面积为
的正三角形.
（1）求椭圆方程；
（2）过分别作直线
，
，且
，设与椭圆交于
，
两点，与椭圆交于
，
两点，求四边形
面积的最小值.
【答案】（1）
；（2）
【解析】
（1）根据题意，分析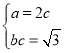可得
，计算可得
、
的值，将、的值代入椭圆的方程即可得答案；
（2）根据题意，分直线的斜率存在、不存在两种情况讨论，借助根与系数的关系分析可得四边形
面积，综合即可得答案．
解：（1）由题设可得：，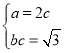
，
，
，
故椭圆方程为；
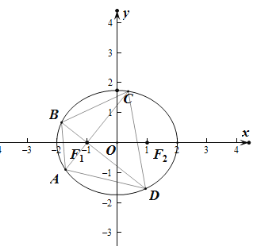
（2）由（1）可知椭圆的焦点
当其中一条直线斜率不存在时，令
，则
当直线斜率存在时，设直线
，
代入椭圆方程得：
，
则
，
；
所以弦长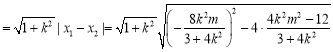
，
设直线
的斜率为
，不妨设
，则
，
，
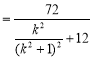
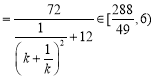
因为，
，
，
，
，
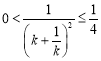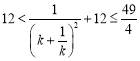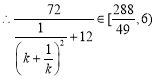
综上，四边形面积的取值范围是
．
故
【题目】“读书可以让人保持思想活跃，让人得到智慧启发，让人滋养浩然之气”，2018年第一期中国青年阅读指数数据显示，从供给的角度，文学阅读域是最多的，远远超过了其他阅读域的供给量.某校采用分层抽样的方法从1000名文科生和2000名理科生中抽取300名学生进行了在暑假阅读内容和阅读时间方面的调查，得到数据如表：
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 130 | ||
文科生 | 45 | ||
合计 |
（1）先完成上面的表格，并判断能否有90%的把握认为学生所学文理与阅读内容有关？
（2从300名被调查的学生中，随机进取30名学生，整理其日平均阅读时间（单位：分钟）如表：
阅读时间 |
|
|
|
|
|
男生人数 | 2 | 4 | 3 | 5 | 2 |
女生人数 | 1 | 3 | 4 | 3 | 3 |
试估计这30名学生日阅读时间的平均值（同一组中的数据以这组数据所在区间中点的值作代表）
（3）从（2）中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得，求这两人都是女生的概率.
参考公式：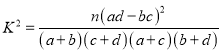 
，其中
.
参考数据：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某大学餐饮中心为了了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如下表所示：
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
根据表中数据，问是否有
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率．
附：
|
|
|
|
|
|
|
|
|
|
