题目内容
【题目】设![]() 是定义在
是定义在![]() 上的函数,若存在
上的函数,若存在![]() ,使得
,使得![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,则称
上单调递减,则称![]() 为
为![]() 上的单峰函数,
上的单峰函数,![]() 为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:
为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:![]() .
.
(1)判断下列函数中,哪些是“![]() 上的单峰函数”?若是,指出峰点;若不是,说出原因;
上的单峰函数”?若是,指出峰点;若不是,说出原因;![]() ;
;
(2)若函数![]() 是
是![]() 上的单峰函数,求实数
上的单峰函数,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 是区间
是区间![]() 上的单峰函数,证明:对于任意的
上的单峰函数,证明:对于任意的![]() ,若
,若![]() ,则
,则![]() 为含峰区间;若
为含峰区间;若![]() ,则
,则![]() 为含峰区间;试问当
为含峰区间;试问当![]() 满足何种条件时,所确定的含峰区间的长度不大于0.6.
满足何种条件时,所确定的含峰区间的长度不大于0.6.
【答案】(1)见解析(2)![]() (3)证明见解析;
(3)证明见解析;
【解析】
(1)画出四个函数图像,根据图像集合单峰函数的定义进行判断.
(2)利用![]() 的导函数
的导函数![]() 的零点在区间
的零点在区间![]() 列不等式,解不等式求得
列不等式,解不等式求得![]() 的取值范围.
的取值范围.
(3)分成![]() 、
、![]() 两种情况进行分类讨论,利用反证法证得结论成立.根据含峰区间的长度的概念列不等式,由此确定
两种情况进行分类讨论,利用反证法证得结论成立.根据含峰区间的长度的概念列不等式,由此确定![]() 满足的条件.
满足的条件.
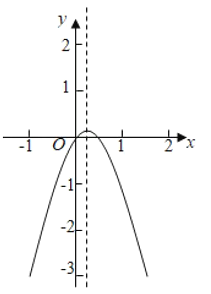
(1)①![]() 图像如下图所示,其对称轴为
图像如下图所示,其对称轴为![]() ,由图可知,
,由图可知,![]() 是
是![]() 上的单峰函数,峰点为
上的单峰函数,峰点为![]() ;
;
②![]() 的图像如下图所示,其对称轴为
的图像如下图所示,其对称轴为![]() ,由图可知,
,由图可知,![]() 是
是![]() 上的单峰函数,峰点为
上的单峰函数,峰点为![]() ;
;

③![]() 的图像如下图所示,根据图像可知,
的图像如下图所示,根据图像可知,![]() 不是
不是![]() 上的单峰函数;
上的单峰函数;

④![]() 的图像如下图所示,其对称轴为
的图像如下图所示,其对称轴为![]() ,由图可知,
,由图可知,![]() 是
是![]() 上的单峰函数,峰点为
上的单峰函数,峰点为![]() .
.

(2)函数![]() 是
是![]() 上的单峰函数,令
上的单峰函数,令![]() ,解得
,解得![]() ,故
,故![]() 时,
时,![]() 递增,
递增,![]() 时,
时,![]() 递减,所以
递减,所以![]() ,解得
,解得![]() ,故
,故![]() 的取值范围是
的取值范围是![]() .
.
(3)设![]() 为
为![]() 的峰点,则由单峰函数定义可知,
的峰点,则由单峰函数定义可知,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
当![]() 时,假设
时,假设![]() ,则
,则![]() ,从而
,从而![]() ,与
,与![]() 矛盾,所以
矛盾,所以![]() ,即
,即![]() 是含峰区间.
是含峰区间.
当![]() 时,假设
时,假设![]() ,则
,则![]() ,从而
,从而![]() ,与
,与![]() 矛盾,所以
矛盾,所以![]() ,即
,即![]() 是含峰区间.
是含峰区间.
在所得的含峰区间内选取![]() ,由
,由![]() 与
与![]() 或
或![]() 与
与![]() ,确定一个新的含峰区间,对先选择的
,确定一个新的含峰区间,对先选择的![]() ,
,![]() ,
,![]() ①,在第一次确定的含峰区间为
①,在第一次确定的含峰区间为![]() 的情况下,
的情况下,![]() 的取值应满足
的取值应满足![]() ②,由①②可得
②,由①②可得 ,当
,当![]() 时,含峰区间的长度为
时,含峰区间的长度为![]() .
.
由条件![]() ,得
,得![]() ,从而
,从而![]() .因此确定的含峰区间的长度不大于
.因此确定的含峰区间的长度不大于![]() ,只要取
,只要取 .
.

练习册系列答案
相关题目


