题目内容
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,
,![]() 且
且![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,试求
,试求![]() ,
,![]() 的值;
的值;
(2)若![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.(用
的取值范围.(用![]() 来表示)
来表示)
【答案】(1)![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)求得二次函数的对称轴,根据对称轴和区间的位置关系,分类讨论,待定系数即可求得![]() ;
;
(2)对参数![]() 进行分类讨论,利用对勾函数的单调性,求得函数的最值,即可容易求得参数范围.
进行分类讨论,利用对勾函数的单调性,求得函数的最值,即可容易求得参数范围.
(1)由题可知![]() 是开口向下,对称轴为
是开口向下,对称轴为![]() 的二次函数,
的二次函数,
当![]() 时,二次函数在区间
时,二次函数在区间![]() 上单调递增,
上单调递增,
故可得![]() 显然不符合题意,故舍去;
显然不符合题意,故舍去;
当![]() ,二次函数在
,二次函数在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
且当![]() 时,取得最小值,故
时,取得最小值,故![]() ,不符合题意,故舍去;
,不符合题意,故舍去;
当![]() 时,二次函数在
时,二次函数在![]() 处取得最小值,在
处取得最小值,在![]() 时取得最大值.
时取得最大值.
则![]() ;
;![]() ,整理得
,整理得![]() ;
;
则![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
故可得![]() .
.
综上所述:![]() .
.
(2)由题可知![]() ,
,
因为![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,且
,且![]() .
.
因为![]() ,故可得
,故可得![]() .
.
①当![]() ,即
,即![]() 时,
时,
![]() 在区间
在区间![]() 单调递减,
单调递减,
故![]() ,
,![]()
则![]() ,
,
解得![]() .
.
此时,![]() ,也即
,也即![]() ,
,
故![]() .
.
②当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() ,即
,即![]()
又因为![]() ,
,![]() ,
,
则![]() ,
,
故![]() 的最大值为
的最大值为![]() ,
,
则![]() ,解得
,解得![]() ,
,
此时![]() ,
,
故可得![]() .
.
综上所述:
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,现收集了该种药用昆虫的
有关,现收集了该种药用昆虫的![]() 组观测数据如下表:
组观测数据如下表:
温度 |
|
|
|
|
|
|
产卵数 |
|
|
|
|
|
|
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为观测数据中的温差和产卵数,
分别为观测数据中的温差和产卵数, ![]() .
.
(1)若用线性回归方程,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到
(精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 回归方程为
回归方程为![]() ,且相关指数
,且相关指数![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
(ii)用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为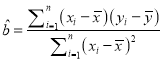 ,
, ![]() ;相关指数
;相关指数
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度,某中学团委以问卷形式调查了![]() 位家长,得到如下统计表:
位家长,得到如下统计表:
男性家长 | 女性家长 | 合计 | |
赞成 |
|
|
|
无所谓 |
|
|
|
合计 |
|
|
|
(1)据此样本,能否有![]() 的把握认为“接受程度”与家长性别有关?说明理由;
的把握认为“接受程度”与家长性别有关?说明理由;
(2)学校决定从男性家长中按分层抽样方法选出![]() 人参加今年的高中学生成人礼仪式,并从中选
人参加今年的高中学生成人礼仪式,并从中选![]() 人交流发言,求发言人中至多一人持“赞成”态度的概率..
人交流发言,求发言人中至多一人持“赞成”态度的概率..
参考数据
|
|
|
|
|
|
参考公式

