题目内容
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.

(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
【答案】(1)![]() ,定义域为
,定义域为![]() ;
;
(2)当![]() 米时,铺路总费用最低,最低总费用为
米时,铺路总费用最低,最低总费用为![]() 元.
元.
【解析】
(1)利用勾股定理通过![]() ,得出
,得出![]() ,结合实际情况得出该函数的定义域;
,结合实际情况得出该函数的定义域;
(2)设![]() ,由题意知,要使得铺路总费用最低,即为求
,由题意知,要使得铺路总费用最低,即为求![]() 的周长
的周长![]() 最小,求出
最小,求出![]() 的取值范围,根据该函数的单调性可得出
的取值范围,根据该函数的单调性可得出![]() 的最小值.
的最小值.
(1)由题意,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
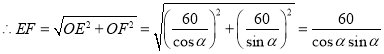 ,
,
所以![]() ,即
,即![]() .
.
当点![]() 在点
在点![]() 时,这时角
时,这时角![]() 最小,求得此时
最小,求得此时![]() ;
;
当点![]() 在
在![]() 点时,这时角
点时,这时角![]() 最大,求得此时
最大,求得此时![]() .
.
故此函数的定义域为![]() ;
;
(2)由题意知,要求铺路总费用最低,只需要求![]() 的周长
的周长![]() 的最小值即可.
的最小值即可.
由(1)得![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
则 ,
,
由![]() ,得
,得![]() ,
,![]() ,则
,则![]() ,
,
从而![]() ,当
,当![]() ,即当
,即当![]() 时,
时,![]() ,
,
答:当![]() 米时,铺路总费用最低,最低总费用为
米时,铺路总费用最低,最低总费用为![]() 元.
元.

【题目】某校进行文科、理科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.

(Ⅰ)根据数学成绩的频率分布表,求理科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:

参考公式与临界值表: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度,某中学团委以问卷形式调查了![]() 位家长,得到如下统计表:
位家长,得到如下统计表:
男性家长 | 女性家长 | 合计 | |
赞成 |
|
|
|
无所谓 |
|
|
|
合计 |
|
|
|
(1)据此样本,能否有![]() 的把握认为“接受程度”与家长性别有关?说明理由;
的把握认为“接受程度”与家长性别有关?说明理由;
(2)学校决定从男性家长中按分层抽样方法选出![]() 人参加今年的高中学生成人礼仪式,并从中选
人参加今年的高中学生成人礼仪式,并从中选![]() 人交流发言,求发言人中至多一人持“赞成”态度的概率..
人交流发言,求发言人中至多一人持“赞成”态度的概率..
参考数据
|
|
|
|
|
|
参考公式



