题目内容
【题目】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先利用直线和圆相切求出圆的方程,再利用平面向量共线和“相关点法”求曲线![]() 的方程;(2)利用两直线间的垂直关系设出直线方程,再联立直线和椭圆的方程,得到关于
的方程;(2)利用两直线间的垂直关系设出直线方程,再联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系和三角形的面积公式得到表达式,再利用基本不等式求其最值.
的一元二次方程,利用根与系数的关系和三角形的面积公式得到表达式,再利用基本不等式求其最值.
试题解析:(1)设动点![]() ,
, ![]() ,因为
,因为![]() 轴于
轴于![]() ,所以
,所以![]() ,
,
由题意得: ![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
由题意, ![]() ,所以
,所以![]() ,
,
所以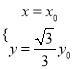 ,即
,即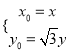
将![]() 代入圆
代入圆![]() ,得动点
,得动点![]() 的轨迹方程
的轨迹方程![]() .
.
(2)由题意可设直线![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() ,
,
联立方程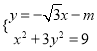 ,得
,得![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,
又因为点![]() 到直线
到直线![]() 的距离
的距离![]() ,
, ![]() ,
,
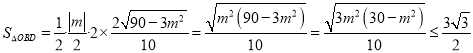 .
.
(当且仅当![]() ,即
,即![]() 时取到最大值)
时取到最大值)
∴![]() 面积的最大值为
面积的最大值为![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据:![]() ,
,![]() )
)
【题目】下列四个命题中错误的是( )
A. 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样
B. 对一个样本容量为100的数据分组,各组的频数如下:
区间 |
|
|
|
|
|
|
|
|
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的![]()
C. 设产品产量与产品质量之间的线性相关系数为![]() ,这说明二者存在着高度相关
,这说明二者存在着高度相关
D. 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表.
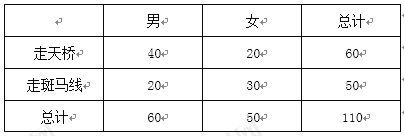
由![]() ,则有
,则有![]() 以上的把握认为“选择过马路方式与性别有关”
以上的把握认为“选择过马路方式与性别有关”