题目内容
AD=2,PA=2,PD=2
 ,∠PAB=60°。
,∠PAB=60°。(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P-BD-A的大小。
(1)在△PAD中,PA=2,AD=2,PD=2 ,可得PA2+AD2=PD2故AD⊥PA
,可得PA2+AD2=PD2故AD⊥PA
又∵AD⊥AB,PA∩AB=A
∴AD⊥平面PAB
(2)∵BC∥AD,∴∠PCB是异面直线PC与AD所成的角。
在△PAB中,由余弦定理得PB= =
=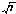
∵AD⊥平面PAB,∴BC⊥平面PAB
∴△PBC为直角三角形
故 tan∠PCB=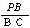 =
=
异面直线PC与AD所成的角为arc tan
(3)过点P作PH⊥AB于H,过点H作HE⊥BD于E,连 接PE。
接PE。
∵AD⊥平面PAB AD 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD
又 PH⊥AB 则PH⊥平面ABCD
∴HE是PE在平面ABCD内的射影
∵BD⊥HE ∴BD⊥PE(三垂线定理)
故∠PEH是二面角P-BD-A的平面角
PH=PA·sin60°= ,AH=PA·cos60°=1
,AH=PA·cos60°=1
BH=AB-AH=2,BD= =
=
由Rt△PEH∽Rt△BAD 得HE= ·BH =
·BH =
在Rt△PHE中,tan∠PEH = =
= 
所以二面角P-BD-A的大小为arc tan
 ,可得PA2+AD2=PD2故AD⊥PA
,可得PA2+AD2=PD2故AD⊥PA又∵AD⊥AB,PA∩AB=A
∴AD⊥平面PAB
(2)∵BC∥AD,∴∠PCB是异面直线PC与AD所成的角。
在△PAB中,由余弦定理得PB=
 =
=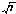
∵AD⊥平面PAB,∴BC⊥平面PAB
∴△PBC为直角三角形
故 tan∠PCB=
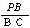 =
=
异面直线PC与AD所成的角为arc tan

(3)过点P作PH⊥AB于H,过点H作HE⊥BD于E,连
 接PE。
接PE。∵AD⊥平面PAB AD
 平面ABCD
平面ABCD∴平面PAB⊥平面ABCD
又 PH⊥AB 则PH⊥平面ABCD
∴HE是PE在平面ABCD内的射影
∵BD⊥HE ∴BD⊥PE(三垂线定理)
故∠PEH是二面角P-BD-A的平面角
PH=PA·sin60°=
 ,AH=PA·cos60°=1
,AH=PA·cos60°=1BH=AB-AH=2,BD=
 =
=
由Rt△PEH∽Rt△BAD 得HE=
 ·BH =
·BH =
在Rt△PHE中,tan∠PEH =
 =
= 
所以二面角P-BD-A的大小为arc tan

略

练习册系列答案
相关题目
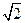 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.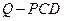 的体积为
的体积为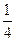 ?若存在,求出
?若存在,求出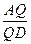 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。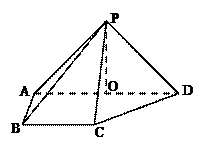
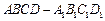 中,
中,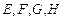 分别是棱
分别是棱 的中点.
的中点.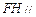 平面
平面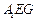 ;
;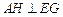 ;
;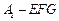 的体积.
的体积.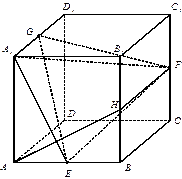
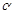 外一点,和平面
外一点,和平面 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。 
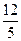 B
B
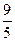 C.
C.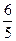 D.
D.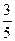
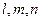 是三条不重合的直线,
是三条不重合的直线,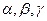 是三个不重合的平面,给出下列四个命题:
是三个不重合的平面,给出下列四个命题: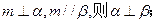
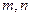 与平面
与平面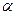 所成的角相等,则
所成的角相等,则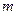 //
//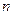 ;
;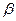 ,
,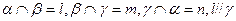 ,则
,则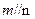 ;
;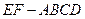 中,
中,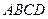 是梯形,
是梯形,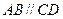 ,
,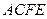 是矩形,面
是矩形,面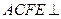 面
面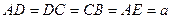 ,
,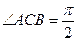 .
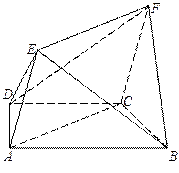
.
 是棱
是棱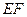 上一点,
上一点,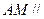 平面
平面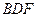 ,求
,求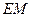 ;
;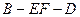 的平面角的余弦值.
的平面角的余弦值.