题目内容
20．
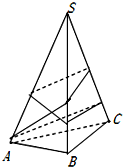已知侧棱长为2的正三棱锥S-ABC如图所示，其侧面是顶角为20°的等腰三角形，一只蚂蚁从点A出发，围绕棱锥侧面爬行两周后又回到点A，则蚂蚁爬行的最短路程为$2\sqrt{3}$．
分析 由题意，利用侧面展开图两次，则顶角为120°，利用余弦定理可得蚂蚁爬行的最短路程．
解答 解：由题意，利用侧面展开图两次，则顶角为120°，
利用余弦定理可得蚂蚁爬行的最短路程为$\sqrt{4+4-2×2×2×（-\frac{1}{2}）}$=$2\sqrt{3}$．
故答案为：$2\sqrt{3}$．
点评 本题考查利用侧面展开图求最短路程，考查余弦定理的运用，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
12．设x为实数，命题p：?x∈R，x2+x+1≥0的否定是（ ）
| A． | ￢p：?x0∈R，x02+x0+1＜0 | B． | ￢p：?x0∈R，x02+x0+1≤0 | ||
| C． | ￢p：?x0∈R，x02+x0+1＜0 | D． | ￢p：?x0∈R，x02+x0+1≤0 |
9．不等式$\frac{{-{x^2}-2x+3}}{x+1}$≥0的解集为（ ）
| A． | {x|x≥3或-1≤x≤1} | B． | {x|x≥3或-1＜x≤1} | C． | {x|x≤-3或-1≤x≤1} | D． | {x|x≤-3或-1＜x≤1} |
10．如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）
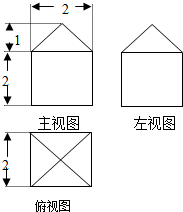
| A． | $（20+4\sqrt{3}）c{m^2}$ | B． | $（20+4\sqrt{2}）c{m^2}$ | C． | $（20+\sqrt{2}）c{m^2}$ | D． | $（10+4\sqrt{2}）c{m^2}$ |