题目内容
已知椭圆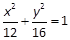 ,则以点
,则以点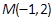 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).
A. | B. |
C. | D.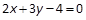 |
C
解析试题分析:设弦的两端点为A(x1,y1),B(x2,y2),
代入椭圆得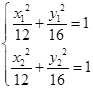 ,
,
两式相减得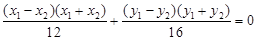 ,整理得
,整理得
∴弦所在的直线的斜率为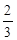 ,其方程为y-2=
,其方程为y-2=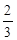 (x+1),整理得
(x+1),整理得 .故选C.
.故选C.
考点:椭圆的性质以及直线与椭圆的关系.在解决弦长的中点问题,常用“点差法”设而不求.

练习册系列答案
相关题目
已知抛物线关于 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点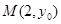 ,若点
,若点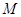 到该抛物线焦点的距离为3,则
到该抛物线焦点的距离为3,则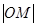 =( )
=( )
A.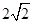 | B.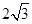 | C.4 | D.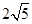 |
已知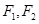 是椭圆和双曲线的公共焦点,
是椭圆和双曲线的公共焦点, 是他们的一个公共点,且
是他们的一个公共点,且 ,则椭圆和双曲线的离心率的倒数之和的最大值为( )
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A.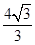 | B. | C.3 | D.2 |
已知椭圆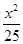 +
+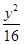 =1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
| A.P点有两个 | B.P点有四个 |
| C.P点不一定存在 | D.P点一定不存在 |
设A1,A2是椭圆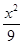 +
+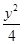 =1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
=1的长轴两个端点,P1,P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
A.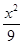 + +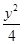 =1 =1 | B.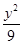 + +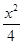 =1 =1 |
C.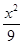 - -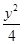 =1 =1 | D.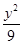 - -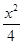 =1 =1 |
 、
、 分别是椭圆
分别是椭圆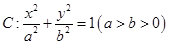 的左、右焦点,点
的左、右焦点,点 在椭圆
在椭圆 上,线段
上,线段 的中点在
的中点在 轴上,若
轴上,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )




 +
+ =1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )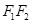 是椭圆
是椭圆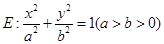 的左、右焦点,
的左、右焦点,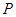 为直线
为直线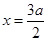 上一点,
上一点, 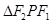 是底角为
是底角为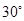 的等腰三角形,则
的等腰三角形,则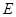 的离心率为( )
的离心率为( )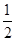
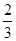
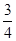
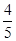
 与抛物线
与抛物线 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).


