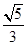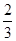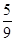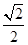题目内容
已知椭圆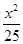 +
+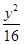 =1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
| A.P点有两个 | B.P点有四个 |
| C.P点不一定存在 | D.P点一定不存在 |
D
解析

练习册系列答案
相关题目
双曲线 的虚轴长等于( )
的虚轴长等于( )
A.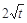 | B.-2t | C. | D.4 |
抛物线 的焦点是( )
的焦点是( )
A. | B. | C. | D. |
已知椭圆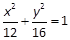 ,则以点
,则以点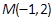 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).
A. | B. |
C. | D.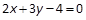 |
椭圆 的离心率为( )
的离心率为( )
A.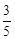 | B.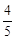 | C.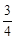 | D.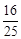 |
设 、
、 两点的坐标分别为
两点的坐标分别为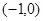 、
、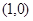 ,条件甲:点
,条件甲:点 满足
满足 ; 条件乙:点
; 条件乙:点 的坐标是方程
的坐标是方程 的解. 则甲是乙的( )
的解. 则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不是充分条件也不是必要条件 |
若直线mx+ny=4与⊙O:x2+y2=4没有交点,则过点P(m,n)的直线与椭圆 +
+ =1的交点个数是( )
=1的交点个数是( )
| A.至多为1 | B.2 | C.1 | D.0 |
对于抛物线y2=4x上任意一点Q,点P(a,0)满足|PQ|≥|a|,则a的取值范围是( )
| A.(-∞,0) | B.(-∞,2] | C.[0,2] | D.(0,2) |
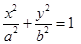
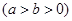 的一个焦点为
的一个焦点为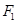 ,若椭圆上存在一个点
,若椭圆上存在一个点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段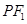 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( )