题目内容
已知双曲线 与抛物线
与抛物线 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).
A. | B. | C. | D. |
A
解析试题分析::∵抛物线 的焦点F(
的焦点F(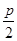 ,0),
,0),
∴由题意知双曲线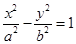 的一个焦点为F(c,0),
的一个焦点为F(c,0),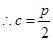 >a,(1)即p>2a.
>a,(1)即p>2a.
∴双曲线方程为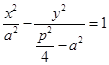 ,
,
∵点M是双曲线与抛物线的一个交点, 若 ,
,
∴p点横坐标xP=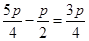 ,代入抛物线y2=8x得P
,代入抛物线y2=8x得P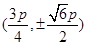 ,把P
,把P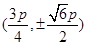 代入双曲线
代入双曲线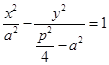 ,得
,得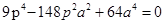 ,
,
解得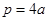 或
或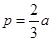 因为p>2a.所以
因为p>2a.所以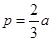 舍去,故
舍去,故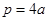 (2)
(2)
联立(1)(2)两式得c=2a,即e=2.故选A.
考点:抛物线的简单性质;双曲线的离心率的求法.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知抛物线关于 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 ,若点
,若点 到该抛物线焦点的距离为3,则
到该抛物线焦点的距离为3,则 =( )
=( )
A. | B.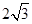 | C.4 | D. |
已知椭圆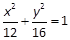 ,则以点
,则以点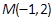 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).
A. | B. |
C. | D.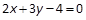 |
抛物线 的准线方程是( )
的准线方程是( )
A. | B. | C. | D. |
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )
A. | B.2 | C. | D. |
若直线mx+ny=4与⊙O:x2+y2=4没有交点,则过点P(m,n)的直线与椭圆 +
+ =1的交点个数是( )
=1的交点个数是( )
| A.至多为1 | B.2 | C.1 | D.0 |
已知双曲线 -
- =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
A.- =1 =1 | B. - - =1 =1 |
C. - - =1 =1 | D. - - =1 =1 |
 的准线与双曲线
的准线与双曲线 交于A,B两点,点F为抛物线的焦点,若
交于A,B两点,点F为抛物线的焦点,若 为直角三角形,则双曲线的离心率是
为直角三角形,则双曲线的离心率是

 =2
=2 ,则点C的轨迹是( )
,则点C的轨迹是( )