题目内容
已知F1、F2是椭圆 +
+ =1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
A.11 B.10 C.9 D.8
A.
解析试题分析:由题意可得: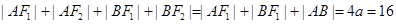 ,
,
∴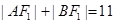 .
.
考点:椭圆的性质.

练习册系列答案
相关题目
双曲线 的虚轴长等于( )
的虚轴长等于( )
A.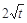 | B.-2t | C. | D.4 |
已知抛物线关于 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 ,若点
,若点 到该抛物线焦点的距离为3,则
到该抛物线焦点的距离为3,则 =( )
=( )
A. | B.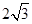 | C.4 | D. |
抛物线 的焦点是( )
的焦点是( )
A. | B. | C. | D. |
已知椭圆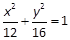 ,则以点
,则以点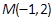 为中点的弦所在直线方程为( ).
为中点的弦所在直线方程为( ).
A. | B. |
C. | D.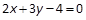 |
设 、
、 两点的坐标分别为
两点的坐标分别为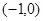 、
、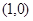 ,条件甲:点
,条件甲:点 满足
满足 ; 条件乙:点
; 条件乙:点 的坐标是方程
的坐标是方程 的解. 则甲是乙的( )
的解. 则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不是充分条件也不是必要条件 |
 的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ).
的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ). C.
C. D.
D.
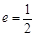 ,则椭圆的标准方程为( ).
,则椭圆的标准方程为( ).


