题目内容
18.数列{an}的前n项和为Sn,且$2{S_n}={a_n}+\frac{1}{3^n}(n∈{N^*}),{b_n}=\frac{1}{{|{a_n}|}}(n∈{N^*})$.(1)求数列{an}的通项公式an;
(3)求证:对任意x>0,${b_n}≥\frac{2}{{{{({e^x}-1)}^2}}}[{e^x}-\frac{1}{4}(5+{(-\frac{1}{3})^n})](e$为自然对数的底数).
分析 (1)利用Sn-Sn-1=an,推出数列$\left\{{{a_n}+\frac{1}{{2×{3^n}}}}\right\}$是以$\frac{1}{2}$为首项、-1为公比的等比数列,然后求解通项公式.
(2)利用已知条件推出${b}_{n}=\frac{2}{1+{(-\frac{1}{3})}^{n}}$,设$m=1+{(-\frac{1}{3})^n}(n∈{N^*})⇒{b_n}=\frac{2}{m}(m>0)$,构造函数$f(x)=\frac{2}{{{{({e^x}-1)}^2}}}[{e^x}-(\frac{5}{4}+{(-\frac{1}{3})^n})](x>0),t=\frac{1}{{{e^x}-1}}(t>0)$,然后证明${b}_{n}≥\frac{2}{{({e}^{x}-1)}^{2}}[{e}^{x}-\frac{1}{4}(5+{(-\frac{1}{3})}^{n})]$.
解答 (1)解:当n=1时,$2{S_1}=2{a_1}={a_1}+\frac{1}{3}⇒{a_1}=\frac{1}{3}$,当n≥2时,$\left\{\begin{array}{l}2{S_n}={a_n}+\frac{1}{3^n}\\ 2{S_{n-1}}={a_{n-1}}+\frac{1}{{{3^{n-1}}}}\end{array}\right.⇒2({S_n}-{S_{n-1}})=2{a_n}={a_n}-{a_{n-1}}+\frac{1}{3^n}-\frac{1}{{{3^{n-1}}}}⇒{a_n}=-{a_{n-1}}-\frac{2}{3^n}(n≥2)$$⇒{a_n}+\frac{1}{{2×{3^n}}}=-({a_{n-1}}+\frac{1}{{2×{3^{n-1}}}}),{a_1}+\frac{1}{2×3}=\frac{1}{2}$,
所以数列$\left\{{{a_n}+\frac{1}{{2×{3^n}}}}\right\}$是以$\frac{1}{2}$为首项、-1为公比的等比数列,
因此${a_n}+\frac{1}{{2×{3^n}}}=\frac{1}{2}{(-1)^{n-1}}⇒$${a_n}=\frac{1}{2}[{(-1)^{n-1}}-\frac{1}{3^n}]$
(2)证明:∵${a_n}=-\frac{1}{2}[{(-1)^n}+\frac{1}{3^n}]⇒{b_n}=\frac{1}{{|{a_n}|}}=\frac{{2×{3^n}}}{{|{1+{{(-3)}^n}}|}}=2×|{\frac{{{{(-3)}^n}}}{{1+{{(-3)}^n}}}}|=\frac{2}{{1+{{(-\frac{1}{3})}^n}}}$,
设$m=1+{(-\frac{1}{3})^n}(n∈{N^*})⇒{b_n}=\frac{2}{m}(m>0)$,
令函数$f(x)=\frac{2}{{{{({e^x}-1)}^2}}}[{e^x}-(\frac{5}{4}+{(-\frac{1}{3})^n})](x>0),t=\frac{1}{{{e^x}-1}}(t>0)$,因为$f(x)=\frac{2}{{{{({e^x}-1)}^2}}}[({e^x}-1)-\frac{1}{4}(1+{(-\frac{1}{3})^n})]=\frac{2}{{{e^x}-1}}-\frac{1}{{2{{({e^x}-1)}^2}}}[1+{(-\frac{1}{3})^n}]$,
所以$f(x)=g(t)=-\frac{m}{2}{t^2}+2t=-\frac{m}{2}{(t-\frac{2}{m})^2}+\frac{2}{m}≤\frac{2}{m}={b_n}$.
点评 本题考查数列数列的判定,数列与函数相结合的应用,考查分析问题解决问题的能力.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
| A. | log52 | B. | log32 | C. | log23 | D. | 都有可能 |
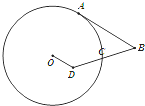 如图,AB与圆O相切于点A,又点D在圆内,DB与圆相交于点C,若BC=DC=3,OD=2,AB=6,那么该圆的半径的长为$\sqrt{22}$.
如图,AB与圆O相切于点A,又点D在圆内,DB与圆相交于点C,若BC=DC=3,OD=2,AB=6,那么该圆的半径的长为$\sqrt{22}$.