题目内容
8.已知函数f(x)=logax(a>0,a≠1),且f(3)-f(2)=1.(1)若f(3m-2)<f(2m+5),求实数m的取值范围.
(2)求使f(x-$\frac{2}{x}$)=$lo{g}_{\frac{3}{2}}\frac{7}{2}$成立的x的值.
分析 (1)先根据对数的运算法则,求出a的值,再根据对数函数的单调性得到关于m的不等式组,解的即可,
(2)根据对数函数的运算性质,即可求出x的值.
解答 解:(1)函数f(x)=logax(a>0,a≠1),且f(3)-f(2)=1,
∴loga3-loga2=1,
∴loga$\frac{3}{2}$=1,
∴a=$\frac{3}{2}$,
∵f(3m-2)<f(2m+5),
∴$\left\{\begin{array}{l}{3m-2>0}\\{2m+5>0}\\{3m-2<2m+5}\end{array}\right.$,
解得:$\frac{2}{3}$<m<7,
∴实数m的取值范围为($\frac{2}{3}$,7).
(2)f(x-$\frac{2}{x}$)=$lo{g}_{\frac{3}{2}}\frac{7}{2}$,
∴$lo{g}_{\frac{3}{2}}$(x-$\frac{2}{x}$)=$lo{g}_{\frac{3}{2}}\frac{7}{2}$,
∴$\left\{\begin{array}{l}{x-\frac{2}{x}>0}\\{x-\frac{2}{x}=\frac{7}{2}}\end{array}\right.$,
解的x=-$\frac{1}{2}$或x=4.
点评 本题考查了对数的运算性质和对数函数的性质,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
18.设集合A={a,b},则满足A∪B={a,b,c}的集合B的个数为( )
| A. | 8 | B. | 4 | C. | 3 | D. | 1 |
16.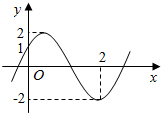 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(1)+f(2)+…+f(2015)的值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(1)+f(2)+…+f(2015)的值为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(1)+f(2)+…+f(2015)的值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(1)+f(2)+…+f(2015)的值为( )| A. | -1 | B. | $\frac{7\sqrt{2}}{2}$ | C. | 671 | D. | 2015 |
13.向边长分别为5,5,6的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{24}$ | C. | 1-$\frac{π}{12}$ | D. | 1-$\frac{π}{24}$ |