题目内容
【题目】如图,等腰直角![]() 中
中![]() 是直角,平面
是直角,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由![]() 及
及![]() 为直角可得到
为直角可得到![]() ,结合已知条件命题得证。
,结合已知条件命题得证。
(2)作![]() ,连结
,连结![]() .由(1)得:
.由(1)得: ![]() ,作
,作![]() ,再证得:
,再证得:![]() 平面
平面![]() ,则
,则![]() 即为所求线面角. 解三角形BFH即可。
即为所求线面角. 解三角形BFH即可。
解:(1)证明:直角![]() 中∠B是直角,即
中∠B是直角,即![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() .
.
(2)方法一:作![]() ,连结
,连结![]() .
.
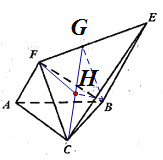
由(1)知![]() 平面
平面![]() ,
,
得到![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
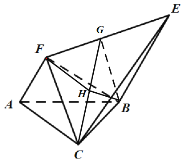
作![]() 于点H,易得
于点H,易得![]() 平面
平面![]() ,
,
则![]() 即为所求线面角.
即为所求线面角.
设![]() ,由已知得
,由已知得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
则直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
方法二:建立如图所示空间直角坐标系![]() ,
,
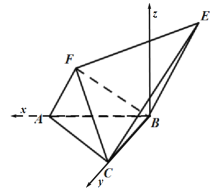
因为![]() .
.
由已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,,
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有
 ,
,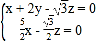 令
令![]() ,则
,则![]() .
.
即![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
方法三(等积法):设2AF=AB=BE=2,![]() 为等腰三角形,AB=BC=2
为等腰三角形,AB=BC=2
∠FAB=60°,2AF=AB ![]() ,又AF//BE,
,又AF//BE,![]() .
.
由(1)知,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,则有
,则有![]() .
.
令![]() 到平面
到平面![]() 距离为
距离为![]() ,有
,有![]() ,
,
故所求线面角![]() .
.

【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业(以下简称外卖甲,外卖乙)的经营情况进行了调查,调查结果如表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单 | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单 | 2.2 | 2.3 | 10 | 5 | 15 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(ⅰ)请用相关系数![]() 加以说明:(若
加以说明:(若![]() ,则可认为
,则可认为![]() 与
与![]() 有较强的线性相关关系(
有较强的线性相关关系(![]() 值精确到0.001))
值精确到0.001))
(ⅱ)经计算求得![]() 与
与![]() 之间的回归方程为
之间的回归方程为![]() .假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(
.假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(![]() 值精确到0.01)
值精确到0.01)
(2)试根据表格中这五天的日接单量情况,从平均值和方差角度说明这两家外卖企业的经营状况.
相关公式:相关系数 ,
,
参考数据:![]()
![]() .
.
【题目】在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是![]() ,到上午10点20分的仰角变成
,到上午10点20分的仰角变成![]() .请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
