题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求证:函数
,求证:函数![]() 有极值;
有极值;
(2)若![]() ,且函数
,且函数![]() 与
与![]() 的图象有两个相异交点,求证:
的图象有两个相异交点,求证:![]() .
.
【答案】(1)见解析.
(2)见解析.
【解析】试题分析:(1)求导数,函数g′(x)有两个零点,则可设为g′(x)=a(x﹣α)(x﹣β),利用零点存在定理,即可证明结论;(2)记h(x)=ex﹣cx﹣c,则h′(x)=ex﹣c,由函数y=f(x)与y=g(x)的图象有两个相异交点知函数h(x)有两互异零点,即可得出结论.
详解:(1)![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() 且
且![]()
∴函数![]() 有两个零点,则可设为
有两个零点,则可设为![]() ,(
,(![]() )
)
∴若![]() ,则
,则![]()
∴![]() 有极值.
有极值.
(2)由![]() ,得
,得![]() ,记
,记![]() ,
,
则![]() ,
,
由函数![]() 与
与![]() 的图象有两个相异交点知函数
的图象有两个相异交点知函数![]() 有两互异零点
有两互异零点
若![]() 单调递增,则
单调递增,则![]() 最多1个零点,矛盾
最多1个零点,矛盾
∴![]() ,此时,令
,此时,令![]() ,则
,则![]() ,列表:
,列表:
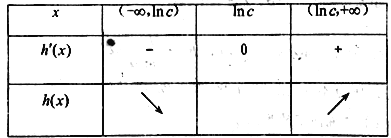
∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目