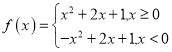题目内容
【题目】设函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() 在
在![]() 上的值域为
上的值域为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
判断f(x)的单调性得出f(x)=k(x+2)在[![]() ,+∞)上有两解,作出函数图象,利用导数的意义求出k的范围.
,+∞)上有两解,作出函数图象,利用导数的意义求出k的范围.
f′(x)=2x﹣lnx+1,f″(x)=2![]() ,
,
∴当x![]() 时,f″(x)≥0,
时,f″(x)≥0,
∴f′(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f′(x)≥f′(![]() )=2﹣ln
)=2﹣ln![]() 0,
0,
∴f(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
∵[a,b][![]() ,+∞),
,+∞),
∴f(x)在[a,b]上单调递增,
∵f(x)在[a,b]上的值域为[k(a+2),k(b+2)],
∴![]() ,
,
∴方程f(x)=k(x+2)在[![]() ,+∞)上有两解a,b.
,+∞)上有两解a,b.
作出y=f(x)与直线y=k(x+2)的函数图象,则两图象有两交点.
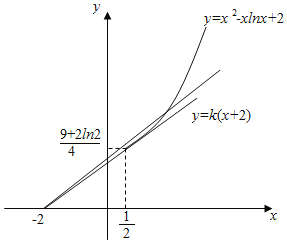
若直线y=k(x+2)过点(![]() ,
,![]() ln2),
ln2),
则k![]() ,
,
若直线y=k(x+2)与y=f(x)的图象相切,设切点为(x0,y0),
则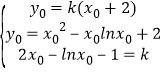 ,解得
,解得![]() k=1.
k=1.
∴1<k![]() ,
,
故选:D.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目