题目内容
【题目】已知曲线C1的参数方程为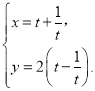
（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝16cosθ.
（1）把曲线C2的极坐标方程化为直角坐标方程；
（2）求C1与C2交点的直角坐标.
【答案】（1）x2+y2＝16x（2）
【解析】
（1）首先利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换.
（2）利用曲线间的位置关系式的应用求出交点的坐标.
（1）由ρ＝16cosθ得，ρ2＝16ρcosθ.
曲线C2的直角坐标方程为x2+y2＝16x.
（2）由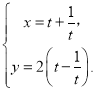
即
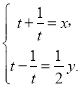得，
，
.
相乘得，曲线C1的直角坐标方程为4x2﹣y2＝16.
由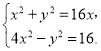
得，5x2﹣16x﹣16＝0.
解得x＝4或
.
x＝4时，y2＝48，
；时，
无实数解.
所以，C1与C2交点的直角坐标为
.
【题目】新型冠状病毒肺炎COVID-19疫情发生以来，在世界各地逐渐蔓延．在全国人民的共同努力和各级部门的严格管控下，我国的疫情已经得到了很好的控制．然而，每个国家在疫情发生初期，由于认识不足和措施不到位，感染确诊人数都会出现加速增长．如表是小王同学记录的某国从第一例新型冠状病毒感染确诊之日开始，连续8天每日新型冠状病毒感染确诊的累计人数．
日期代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染确诊人数的变化趋势，小王同学分别用两种模型：
①
，②
对变量
和
的关系进行拟合，得到相应的回归方程并进行残差分析，残差图如下（注：残差
，且经过计算得
，
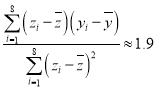，其中
，
，
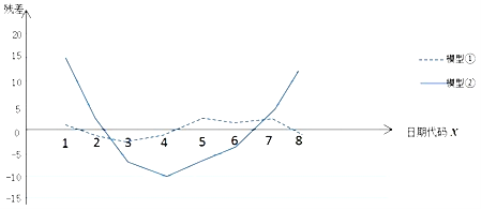
（1）根据残差图，比较模型①，②的拟合效果，应该选择哪个模型？并简要说明理由；
（2）根据（1）中选定的模型求出相应的回归方程；
（3）如果第9天该国仍未采取有效的防疫措施，试根据（2）中所求的回归方程估计该国第9天新型冠状病毒感染确诊的累计人数．（结果保留为整数）
附：回归直线的斜率和截距的最小二乘估计公式分别为：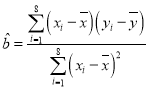
，
．
