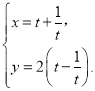题目内容
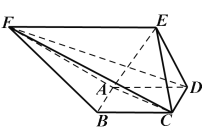
【题目】新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,每个国家在疫情发生初期,由于认识不足和措施不到位,感染确诊人数都会出现加速增长.如表是小王同学记录的某国从第一例新型冠状病毒感染确诊之日开始,连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染确诊人数的变化趋势,小王同学分别用两种模型:
①![]() ,②
,②![]() 对变量
对变量![]() 和
和![]() 的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差
的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差![]() ,且经过计算得
,且经过计算得 ,
,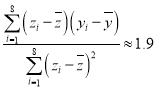 ,其中
,其中![]() ,
,![]() ,
,
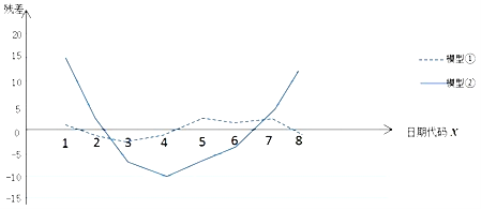
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;
(2)根据(1)中选定的模型求出相应的回归方程;
(3)如果第9天该国仍未采取有效的防疫措施,试根据(2)中所求的回归方程估计该国第9天新型冠状病毒感染确诊的累计人数.(结果保留为整数)
附:回归直线的斜率和截距的最小二乘估计公式分别为: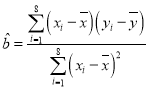 ,
,![]() .
.
【答案】(1)模型①的拟合效果更好,理由详见解析;(2)![]() ;(3)156人.
;(3)156人.
【解析】
(1)根据残差点分布的区域的宽度越狭窄,其模型拟合的精度越高即可得解;
(2)因为![]() ,所以
,所以![]() ,然后结合数据和公式分别算出
,然后结合数据和公式分别算出![]() ,
,![]() ,即可得到
,即可得到![]() 关于
关于![]() 的回归方程,进而得到
的回归方程,进而得到![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)把![]() 代入回归方程算出
代入回归方程算出![]() 即可得解.
即可得解.
(1)因为残差![]() ,所以残差点分布的区域的宽度越狭窄,其模型拟合的精度越高,所以模型①的拟合效果更好.
,所以残差点分布的区域的宽度越狭窄,其模型拟合的精度越高,所以模型①的拟合效果更好.
(2)因为![]() 且
且![]() ,所以
,所以![]() ,
,
由表格中数据可知,![]() ,
,
![]() ,
,
所以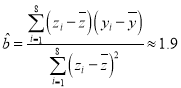 ,
,![]() ,
,
所以![]() ,
,
故所求的回归方程为![]() .
.
(3)当![]() 时,有
时,有![]() ,
,
故估计该国第9天新型冠状病毒感染确诊的累计人数为156人.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() .某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
.某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.