Question

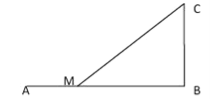
【题目】如图,设铁路长为,且,为将货物从运往,现在上的距点为的点处修一公路至,已知单位距离的铁路运费为,公路运费为.

（1）将总运费表示为的函数；

（2）如何选点才使总运费最小？

Answer 1

【答案】（1）；（2）当在距离点为时的点处修筑公路至时总运费最省．

【解析】

试题分析：（1）有已知中铁路长为，且，为将货物从运往，现在上距点为的点处修一条公路至，已知单位距离的铁路运费为，公路运费为，我们可以计算公路上的运费和铁路上的运费，进而得到由到的总运费；（2）由（1）中所得的总运费表示为的函数，利用导数法，我们可以分析出函数的单调性，以及憨厚的最小值点，得到答案.

试题解析：（1）依题中，铁路长为,且,将货物从运往,现在上的距点为的点处修一公路至,且单位距离的铁路运费为,公路运费为.

铁路上的运费为,公路上的运费为,

则由到的总运费为.

（2）,令,解得,或（舍）.

当时, ；当时, ；

故当时, 取得最小值, 即当在距离点为时的点处修筑公路至时总运费最省.