题目内容
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ).
).
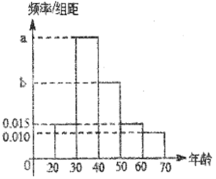
(1)若![]() 的部分图像如图所示,求
的部分图像如图所示,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,求最小正实数![]() ,使得函数
,使得函数![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数是偶函数;
个单位后所对应的函数是偶函数;
(3)若![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的最大值.
的最大值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据函数的图象,即可确定![]() 的值,得到函数的解析式;(2)根据三角函数的平行关系,结合偶函数的性质,即可求得最小正实数
的值,得到函数的解析式;(2)根据三角函数的平行关系,结合偶函数的性质,即可求得最小正实数![]() 的值;(3)根据三角函数的单调性和周期性之间的关系,建立不等关系式,即可求解实数
的值;(3)根据三角函数的单调性和周期性之间的关系,建立不等关系式,即可求解实数![]() 的最大值.
的最大值.
试题解析:(1)![]() ;
;
(2)将![]() 的图象向左平移
的图象向左平移![]() 的单位可得函数
的单位可得函数![]()
![]() 的图象.
的图象.
∵![]() 是偶函数,∴直线
是偶函数,∴直线![]() 是
是![]() 的一条对称轴,
的一条对称轴,
∴![]()
![]() ,∴
,∴![]() ,即
,即![]() (
(![]() ),
),
令![]() 可得最小正实数
可得最小正实数![]() .
.
(3)当![]() 最大时,函数在一个周期内完整单调递增区间就是
最大时,函数在一个周期内完整单调递增区间就是![]() ,
,
故函数周期![]() 满足
满足![]() ,故
,故![]() ,解得
,解得![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目