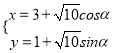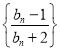题目内容
【题目】已知函数y＝Asin(ωx＋φ)(A>0，ω>0)的图象过点P
，图象与P点最近的一个最高点坐标为
.
(1)求函数解析式；
(2)求函数的最大值，并写出相应的x的值；
(3)求使y≤0时，x的取值范围．
【答案】（1）
（2）
（3）
【解析】试题分析：（1）由最高点可得A＝5，由图象与P点最近的距离可得四分之一个周期，解得ω，最后根据最大值求φ（2）由正弦函数性质确定最大值取法: 
,解方程可得x的值；（3）利用正弦函数性质解三角不等式可得2kπ－π≤2x－
≤2kπ，即得x的取值范围．
试题解析：解：(1)由题意知
＝
－
＝
，∴T＝π.
∴ω＝
＝2，由ω·＋φ＝0，得φ＝－
，又A＝5，
∴y＝5sin
.
(2)函数的最大值为5，此时2x－
＝2kπ＋
(k∈Z)．∴x＝kπ＋
(k∈Z)
(3)∵5sin
≤0，
∴2kπ－π≤2x－≤2kπ(k∈Z)．
∴kπ－
≤x≤kπ＋
(k∈Z)．
练习册系列答案
相关题目
【题目】某日用品按行业质量标准分成五个等级，等级系数X依次为1,2,3,4,5．现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0．2 | 0．45 | b | c |
（1）若所抽取的20件日用品中，等级系数为4的恰有3件，等级系数为5的恰有2件，求a，b，c的值；
（2）在（1）的条件下，将等级系数为4的3件日用品记为
，等级系数为5的2件日用品记为
，现从
， 
这5件日用品中任取两件（假定每件日用品被取出的可能性相同），求这两件日用品的等级系数恰好相等的概率．
