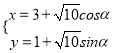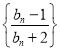题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)在函数![]() 的图象上是否存在不同的两点
的图象上是否存在不同的两点![]() ,使线段
,使线段![]() 的中点的横坐标
的中点的横坐标![]() 与直线
与直线![]() 的斜率
的斜率![]() 之间满足
之间满足![]() ?若存在,求出
?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1) ![]() 取得极大值
取得极大值![]() ,无极小值;(2)
,无极小值;(2) ![]() ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)当![]() 时,求函数的导数以及导数的零点,并判断零点两侧的单调性,求得极值;(2)根据条件将问题转化为
时,求函数的导数以及导数的零点,并判断零点两侧的单调性,求得极值;(2)根据条件将问题转化为![]() ,当
,当![]() 时恒成立,采用参变分离的方法,得到
时恒成立,采用参变分离的方法,得到![]() ;(3)设点A,B的坐标,表示两点连线的斜率,以及中点处的导数,得到
;(3)设点A,B的坐标,表示两点连线的斜率,以及中点处的导数,得到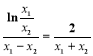 ,可将此式变形为关于
,可将此式变形为关于![]() 的函数,转化为判定函数是否有零点的问题.
的函数,转化为判定函数是否有零点的问题.
试题解析:解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
故![]()
![]()
![]() 单调递增;
单调递增;![]()
![]()
![]() 单调递减,
单调递减,
![]() 时,
时,![]() 取得极大值
取得极大值![]() ,无极小值.
,无极小值.
(2)![]() ,
,![]() ,
,
若函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 对
对![]() 恒成立
恒成立
∴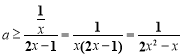 ,只需
,只需![]()
∵![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,
故![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.
(3)假设存在,不妨设![]() ,
,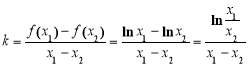
![]()
由![]() 得
得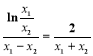 ,整理得
,整理得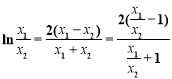
令![]() ,
,![]() ,
,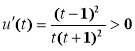
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,故
,故![]() ,
, ![]() 不存在符合题意的两点.
不存在符合题意的两点.

练习册系列答案
相关题目
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。