题目内容
【题目】已知A(4, 0)，B（2, 2），C (6, 0)，记△ABC的外接圆为⊙P．
（1）求⊙P的方程．
（2）对于线段PA上的任意一点G，是否存在以B为圆心的圆，在圆B上总能找到不同的两点E、F，满足
=
，若存在，求圆B的半径
的取值范围；若不存在，说明理由．
【答案】（1）
；（2）
【解析】试题分析：（1）设⊙P的方程为x2＋y2＋Dx＋Ey＋F＝0，将A(4, 0)，B（2, 2），C (6, 0)代入圆方程，解方程组即可得结果；（2）假设存在圆B: 
满足题意， 
，又A(4, 0)， 
PA的直线方程是： 
，设G（m, n）（
），设F(x, y)，则中点
，根据E、F在圆B上可得
，进而可得结果.
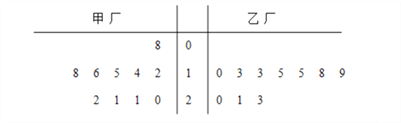
试题解析：(1) 解法一：设⊙P的方程为x2＋y2＋Dx＋Ey＋F＝0．
因为点A，B，C均在所求圆上，所以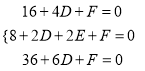
解得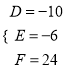
故⊙P的方程是
．
解法二： 
A(4, 0)，B（2, 2），C (6, 0)，
AB的中垂线方程为： 
，①
AC的中垂线方程为： 
,②
联立①②可得圆心
，
半径
，
故⊙P的方程是
．
（2）假设存在圆B: 
满足题意，
，又A(4, 0)，
PA的直线方程是： 
，
设G（m, n）（
）
则有
， 
， 
设F(x, y)，则中点
，
由E、F在圆B上可得：
，
即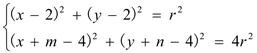
，①
存在E、F即方程组①有解，即圆
与圆
有公共点，
所以
，
把
代入可得
故
对任意
恒成立，
在
上单调递减，在
单调递增，
， 
，
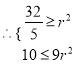，解得
，
又
E为线段GF的中点， E、F在圆B上，
G在圆B外
，即
在
恒成立
练习册系列答案
相关题目
