题目内容
观察:52 – 1 = 24,72 – 1 = 48,112 – 1 = 120,132 – 1 = 168,… 所得的结果都是24的倍数,继续试验,则有( )
| A.第1个出现的等式是:152 – 1 =" 224" |
| B.一般式是:(2n + 3)2 – 1 =" 4(n" + 1)(n+2) |
| C.当试验一直继续下去时,一定会出现等式1012 – 1 =10200 |
| D.24的倍数加1必是某一质数的完全平方 |
C
解:因为52 – 1 = 24,72 – 1 = 48,112 – 1 = 120,132 – 1 = 168,… 所得的结果都是24的倍数,继续试验,则有当试验一直继续下去时,一定会出现等式1012 – 1 =10200,选C

练习册系列答案
相关题目
 中的相邻两项
中的相邻两项 是关于
是关于 的方程
的方程 的两个根,且
的两个根,且 .
. ,
, ,
, ,
, 及
及 (不必证明);
(不必证明); 项和
项和 .
.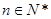 时,令
时,令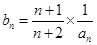 ,
,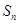 是数列{bn}的前n项和,求证:
是数列{bn}的前n项和,求证: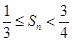
 的前
的前 项和为
项和为 .若
.若 ,
, ,则
,则 ( )
( )



 的前
的前 项和
项和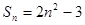 ,则
,则 .
. 中,
中, ,
, ,
, 。
。 ,
, ,
, 的值;
的值;  ,3,
,3, ,…,则
,…,则 可以是这个数列的 ( )
可以是这个数列的 ( ) 当
当 时,观察下列等式:
时,观察下列等式: ,
,  ,
, ,
,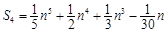 ,
, ,
, .
. 
 的前
的前 项和
项和 ,则
,则 的值是( )
的值是( )


