��Ŀ����
����Ŀ����ͼ����֪˫����C1�� ![]() ������C2��|y|=|x|+1��P��ƽ����һ�㣬�����ڹ���P��ֱ����C1 �� C2���й����㣬���PΪ��C1��C2�͵㡱
������C2��|y|=|x|+1��P��ƽ����һ�㣬�����ڹ���P��ֱ����C1 �� C2���й����㣬���PΪ��C1��C2�͵㡱 
��1������ȷ֤��C1�����ǡ�C1��C2�͵㡱ʱ��Ҫʹ��һ�����ý����ֱ�ߣ���д��һ��������ֱ�ߵķ��̣���Ҫ����֤����
��2����ֱ��y=kx��C2�й����㣬��֤|k|��1������֤��ԭ�㲻�ǡ�C1��C2�͵㡱��
��3����֤��Բx2+y2= ![]() �ڵĵ㶼���ǡ�C1��C2�͵㡱
�ڵĵ㶼���ǡ�C1��C2�͵㡱
���𰸡�
��1���⣺C1����Ϊ�� ![]() ����д����ֱ�߷��̿�����������ʽ��
����д����ֱ�߷��̿�����������ʽ��
![]() ��
�� ![]() ������
������ ![]()
��2��֤������Ϊֱ��y=kx��C2�й����㣬
���Է����� ![]() ��ʵ���⣬���|kx|=|x|+1����
��ʵ���⣬���|kx|=|x|+1���� ![]() ��
��
��ԭ���ǡ�C1��C2�͵㡱������ڹ�ԭ���ֱ����C1��C2���й����㣮
���ǹ�ԭ����C2�й������ֱ��x=0��y=kx��|k|��1����
��Ȼֱ��x=0��C1�����㣮
���ֱ��Ϊy=kx��|k|��1�������ɷ����� 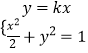 ����
���� ![]() ��ì�ܣ�
��ì�ܣ�
����ֱ��y=kx��|k|��1����C1Ҳ�����㣮
���ԭ�㲻�ǡ�C1��C2�͵㡱
��3��֤������ԲO�� ![]() ��ȡԲO�ڵ�һ��Q�����о���Q��ֱ��l��C1��C2���й����㣬��Ȼl����x�ᴹֱ��
��ȡԲO�ڵ�һ��Q�����о���Q��ֱ��l��C1��C2���й����㣬��Ȼl����x�ᴹֱ��
�ʿ���l��y=kx+b��
��|k|��1������ԲO��������ƽ����y=x��1��y=��x��1֮�䣬���ԲOҲ����ֱ��y=kx��1��y=��kx��1֮�䣬
�Ӷ���Q����kΪб�ʵ�ֱ��l��C2�����㣬ì�ܣ�����|k|��1��
��Ϊl��C1�ɹ����㣬���Է����� 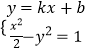 ��ʵ���⣬
��ʵ���⣬
�ã�1��2k2��x2��4kbx��2b2��2=0��
��Ϊ|k|��1������1��2k2��0��
��ˡ�=��4kb��2��4��1��2k2������2b2��2��=8��b2+1��2k2����0��
��b2��2k2��1��
��ΪԲO��Բ�ģ�0��0����ֱ��l�ľ��� ![]() ��
��
���� ![]() ���Ӷ�
���Ӷ� ![]() ����k2��1����|k|��1ì�ܣ�
����k2��1����|k|��1ì�ܣ�
��ˣ�Բ ![]() �ڵĵ㲻�ǡ�C1��C2�͵㡱
�ڵĵ㲻�ǡ�C1��C2�͵㡱
����������1����˫���߷��̿�֪��˫���ߵ���Ϊ�� ![]() �����������ֱ�ߵ�б�ʲ�����ʱ�������ǡ�C1��C2�͵㡱����б�ʴ���ʱ��Ҫ��֤б�ʵľ���ֵ���ڵ��ڸý����루0��1�����ߵ�б�ʣ���2����ֱ��y=kx��C2�й�����������������ʵ����õ�|k|��1���ֹ�ԭ���ֱ��б�ʲ����ں�б�ʴ����������˵����Զ���ֱ�߲�����ͬʱ��C1��C2�й����㣻��3���ɸ�����Բ�ķ��̵õ�Բ��ͼ�μ���ֱ��y=x��1��y=��x��1֮�䣬����˵����|k|��1ʱ��Բ
�����������ֱ�ߵ�б�ʲ�����ʱ�������ǡ�C1��C2�͵㡱����б�ʴ���ʱ��Ҫ��֤б�ʵľ���ֵ���ڵ��ڸý����루0��1�����ߵ�б�ʣ���2����ֱ��y=kx��C2�й�����������������ʵ����õ�|k|��1���ֹ�ԭ���ֱ��б�ʲ����ں�б�ʴ����������˵����Զ���ֱ�߲�����ͬʱ��C1��C2�й����㣻��3���ɸ�����Բ�ķ��̵õ�Բ��ͼ�μ���ֱ��y=x��1��y=��x��1֮�䣬����˵����|k|��1ʱ��Բ ![]() �ڵĵ���б��Ϊk��ֱ����C2�����㣬��|k|��1ʱ����Բ
�ڵĵ���б��Ϊk��ֱ����C2�����㣬��|k|��1ʱ����Բ ![]() �ڵĵ���б��Ϊk��ֱ����C2�й����㣬����Բ�ĵ�ֱ�ߵľ���С�ڰ뾶��ʽ�ó�k�ķ�Χ�������|k|��1ì�ܣ��Ӷ�֤���˽��ۣ�
�ڵĵ���б��Ϊk��ֱ����C2�й����㣬����Բ�ĵ�ֱ�ߵľ���С�ڰ뾶��ʽ�ó�k�ķ�Χ�������|k|��1ì�ܣ��Ӷ�֤���˽��ۣ�
�����㾫����������Ĺؼ���������㵽ֱ�ߵľ��빫ʽ�����֪ʶ�����յ�![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ��
�ľ���Ϊ�� ��
��