题目内容
【题目】用随机模拟的方法估算边长是2的正方形内切圆的面积(如图所示),并估计π的近似值.
【答案】见解析；
【解析】试题分析: 随机模拟的步骤:产生随机数,统计次数,根据古典概型概率公式计算概率,利用几何概型概率计算概率,由两者相等求出π的近似值
试题解析:解:(1)利用计算机产生两组[0,1]上的均匀随机数a1,b1.
(2)平移和伸缩变换,a=(a1-0.5)×2,b=(b1-0.5)×2,得到两组[-1,1]上的均匀随机数.
(3)统计试验总次数N和点落在圆内的次数N1(满足a2+b2≤1的点(a,b)的个数).
(4)计算频率
,即为点落在圆内的概率.
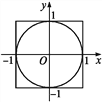
(5)如图,设圆面积为S,则由几何概型概率公式得P=.
所以
,即S≈
,即圆面积的近似值为.
又因为S圆=πr2
点睛:利用随机模拟的方法计算不规则图形的面积的一个常用思路是：在不规则图形外加一个规则图形，利用几何概型的概率公式求出落在所求面积的图形内任意一点的事件发生的概率；再利用随机模拟的方法产生随机数，计算相关频率．当试验次数增加到一定程度，所得的频率就可以看成用几何概型的概率公式求出的概率，进而可求出所求的面积．用类似方法也可求出不规则几何体的体积．
练习册系列答案
名校课堂系列答案
相关题目
