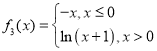题目内容
【题目】已知倾斜角为
的直线经过抛物线
的焦点
，与抛物线
相交于
、
两点，且
.
（1）求抛物线的方程；
（2）求过点
且与抛物线的准线相切的圆的方程.
【答案】（1）
（2）
或
【解析】
（1）设直线
的方程为
与抛物线联立，结合
，利用韦达定理可求解p，即得解；
（2）利用韦达定理，可得的中点为
，可求解AB的垂直平分线的方程，圆心为
，利用圆半径、弦长、弦心距的勾股关系，可求解a，可得圆方程.
解：（1）由题意设直线的方程为，令
、
，
联立
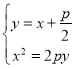得
根据抛物线的定义得
又
， 
故所求抛物线方程为
（2）由（1）知
，
的中点为，的垂直平分线方程为
即
设过点
的圆的圆心为，
该圆与
的准线
相切，
半径
圆心到直线
的距离为
，解得
或
圆心的坐标
为，半径为
，或圆心的坐标为
，半径为
圆的方程为或
练习册系列答案
相关题目
【题目】某乡镇为了发展旅游行业，决定加强宣传，据统计，广告支出费
与旅游收入
（单位：万元）之间有如下表对应数据：
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
（1）求旅游收入对广告支出费的线性回归方程
，若广告支出费
万元，预测旅游收入；
（2）在已有的五组数据中任意抽取两组，根据（1）中的线性回归方程，求至少有一组数据，其预测值与实际值之差的绝对值不超过
的概率.（参考公式：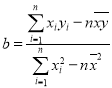
，
，其中
为样本平均值，参考数据：
，
，
）
