题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() 。
。
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围。
的取值范围。

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由椭圆的离心率可得![]() ,根据椭圆过点
,根据椭圆过点![]() 可得
可得![]() ,求得
,求得![]() ,
, ![]() 后可得椭圆的方程.(2)将直线方程代入椭圆方程后整理可得
后可得椭圆的方程.(2)将直线方程代入椭圆方程后整理可得![]() ,由
,由![]() 得
得![]() .由根与系数的关系求得弦MN的中点
.由根与系数的关系求得弦MN的中点![]() ,由此可得直线AG的斜率
,由此可得直线AG的斜率![]() ,根据
,根据![]() 可得
可得![]() ,由此可得
,由此可得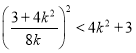 ,解得
,解得![]() ,即为所求范围.
,即为所求范围.
试题解析:
(1)![]() 椭圆的离心率
椭圆的离心率![]() ,
,
![]() ,即
,即![]() ;①
;①
又椭圆过点![]() ,
,
∴![]() ,②
,②
由①②得![]() ,
, ![]() ,
,
∴椭圆的方程为![]() .
.
(2)由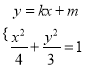 消去
消去![]() 整理得
整理得
![]() ,
,
![]() 直线与椭圆交于不同的两点,
直线与椭圆交于不同的两点,
![]() ,
,
整理得![]() ……(1)
……(1)
设![]() ,弦MN的中点A
,弦MN的中点A![]() ,
,
则![]() ,
,
∴![]()
∴![]() ,
,
∴点A的坐标为![]() ,
,
∴直线AG的斜率为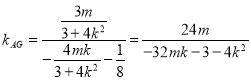 ,
,
又直线AG和直线MN垂直,
∴![]() ,
,
∴![]() ,
,
将上式代入(1)式,可得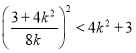 ,
,
整理得![]() ,
,
解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为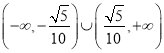 .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目