题目内容
对于任意的x∈R，不等式2x2-a
+3＞0恒成立，则实数a的取值范围是（ ）
| x2+1 |
A．a＜2
| B．a≤2
| C．a＜3 | D．a≤3 |
先从 2x2-a
+3＞0分离出参数a，
即 a＜
恒成立，
下面只要求 y=
的最小值即可，
令
=t（t≥1）则x2=t2-1，
∴y=
=2t+
，
∵y=2t+
在[1，+∞）单调增函数，
∴当t=1时，y有最小值3，
故a＜3，
故答案为：a＜3．
| x2+1 |
即 a＜
| 2x2+3 | ||
|
下面只要求 y=
| 2x2+3 | ||
|
令
| x2+1 |
∴y=
| 2t2+1 |
| t |
| 1 |
| t |
∵y=2t+
| 1 |
| t |
∴当t=1时，y有最小值3，
故a＜3，
故答案为：a＜3．
练习册系列答案
阅读快车系列答案
相关题目
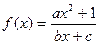（a、b、c∈Z）是奇函数,又
，
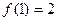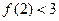，求a、b、c的值.
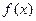定义域是
，则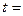
.