题目内容
【题目】已知M( ![]() ,0),N(2,0),曲线C上的任意一点P满足:
,0),N(2,0),曲线C上的任意一点P满足: ![]()
![]() =
= ![]() |
| ![]() |.
|.
(Ⅰ)求曲线C的方程;
(Ⅱ)设曲线C与x轴的交点分别为A、B,过N的任意直线(直线与x轴不重合)与曲线C交于R、Q两点,直线AR与BQ交于点S.问:点S是否在同一直线上?若是,请求出这条直线的方程;若不是,请说明理由.
【答案】解:(Ⅰ)设点P(x,y),∵M( ![]() ,0),N(2,0), ∴
,0),N(2,0), ∴ ![]() =(﹣
=(﹣ ![]() ,0),
,0), ![]() =(x﹣
=(x﹣ ![]() ,y),
,y), ![]() =(2﹣x,﹣y),
=(2﹣x,﹣y),
代入 ![]()
![]() =
= ![]() |
| ![]() |,化简得
|,化简得 ![]() +
+ ![]() =1,
=1,
所以曲线C的方程为 ![]() +
+ ![]() =1;
=1;
(Ⅱ)结论:点S是在同一条直线x= ![]() 上.
上.
理由如下:
(i)当直线的斜率存在时,设直线方程为y=k(x﹣2),
将直线方程代入曲线C: ![]() +
+ ![]() =1中,
=1中,
化简得:(5+9k2)x2﹣36k2x+(36k2﹣45)=0.
设点R(x1 , y1),Q(x2 , y2),利用根与系数的关系得:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
在曲线C的方程中令y=0得x=±3,不妨设A(﹣3,0),B(3,0),
则kBR= ![]() ,则直线BR:y=
,则直线BR:y= ![]() (x﹣3).
(x﹣3).
同理直线 ![]() .
.
由直线方程BR、AQ,消去y,
得x= 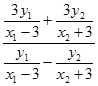 =
= ![]() =
=  =
= ![]() ,
,
所以点S是在直线x= ![]() 上;
上;
(ii)当直线的斜率不存在时,则直线方程为x=2.
可得点S的横坐标为 ![]() .
.
综合(i)(ii)得,点S是在同一条直线x= ![]() 上
上
【解析】(Ⅰ)设点P(x,y),通过M、N点坐标,可得 ![]() 、
、 ![]() 、
、 ![]() 的坐标表示,利用
的坐标表示,利用 ![]()
![]() =
= ![]() |
| ![]() |计算即可;(Ⅱ)当直线的斜率存在时,设直线方程并代入曲线C中,化简后利用韦达定理计算即得结论;当直线的斜率不存在时,即得结论.
|计算即可;(Ⅱ)当直线的斜率存在时,设直线方程并代入曲线C中,化简后利用韦达定理计算即得结论;当直线的斜率不存在时,即得结论.

 阅读快车系列答案
阅读快车系列答案【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式:
![]() .
.

