题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
【答案】(1)![]() .
.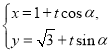 (
(![]() 为参数).(2)
为参数).(2)![]() 或
或![]() .
.
【解析】
(1)曲线![]() 的参数方程消去参数即得普通方程,根据直线参数方程的定义表示即可;
的参数方程消去参数即得普通方程,根据直线参数方程的定义表示即可;
(2)将直线的参数方程代入圆的普通方程,得到韦达定理,由参数方程的几何意义可以得到![]() 即可得解.
即可得解.
(1)由参数方程得![]() ,
,
所以曲线![]() 的普通方程为
的普通方程为![]() .
.
设点![]() 的直角坐标为
的直角坐标为![]() .则
.则![]() ,
,![]() .
.
即![]() ,故直线
,故直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(2)将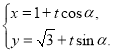 代入
代入![]() ,得
,得![]() .
.
![]() .
.
设![]() 是方程的两个根,则
是方程的两个根,则![]() ,
,![]() .
.
所以![]()
![]() .
.
所以![]()
整理得![]() 或
或![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员,员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种,某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较对40人一月中的顾客评价“不满意“的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:[0,5),[5,10),[10,15),[15,20),[20,25],得到如下频数分布表.
分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;并求出男、女柜员的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员的满意度谁高?
(2)在抽取的40名柜员员工中,从“不满意”次数不少于20的柜员员工中随机抽取3人,求抽取的3人中,男柜员不少于女柜员的概率.
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图茎叶图:

![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
![]() 完成下面的列联表,并根据列联表判断是否有
完成下面的列联表,并根据列联表判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | |
第一阶段 | ||
第二阶段 |
附:![]()
|
|
|
|
k |
|
|
|