题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据题意得到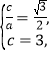 解得
解得![]() ,再由a,b,c的关系得到结果;(2)设出直线AM,联立直线和椭圆,表示出点M的坐标,设直线
,再由a,b,c的关系得到结果;(2)设出直线AM,联立直线和椭圆,表示出点M的坐标,设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,即
,即![]() ,把点
,把点![]() 坐标中
坐标中![]() 的替换为
的替换为![]() ,得到点N的坐标,利用两点坐标表示出直线MN即可得到直线过定点.
,得到点N的坐标,利用两点坐标表示出直线MN即可得到直线过定点.
(1)由题意知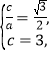 解得
解得![]() .
.
又![]() ,
,
![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
(2)设左顶点![]() ,根据已知得直线
,根据已知得直线![]() 的斜率存在且不为零,
的斜率存在且不为零,
设![]() ,代入椭圆方程,得
,代入椭圆方程,得![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,
即![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,即
,即![]() ,把点
,把点![]() 坐标中
坐标中![]() 的替换为
的替换为![]() ,得
,得![]() .
.
当![]() 的横坐标不相等,即
的横坐标不相等,即![]() 时,
时,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,该直线恒过定点
,该直线恒过定点![]() .
.
当![]() 时,
时,![]() 、
、![]() 的横坐标为零,直线
的横坐标为零,直线![]() 也过定点
也过定点![]() .
.
综上可知,直线![]() 过定点
过定点![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.
【题目】甲、乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击命中目标得
次,射击命中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,从甲、乙两人的
,从甲、乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅲ)在![]() 局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)

