题目内容
求圆心在直线3x+y-5=0上,并且经过原点和点(4,0)的圆的方程
(x-2)2+(y+1)2 =5
解析试题分析:解:设:原点O(0,0)和点A(4,0),
则线段OA的垂直平分线的方程为x=2
所以圆心的坐标为(2,b)
又因为圆心在直线3x+y-5=0上,
所以3×2+b-5="0,b=-1," 圆心的坐标为(2,-1)
r2=22+(-1)2 =5
所以圆的方程为(x-2)2+(y+1)2 =5
考点:圆的方程
点评:本试题主要是考查了圆的方程的求解,属于基础题。

练习册系列答案
相关题目
 过点
过点 ,且圆心
,且圆心 上。
上。 : ①斜率为
: ①斜率为 ;②直线被圆
;②直线被圆 ,以
,以 过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.
过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由. 及直线
及直线 . 当直线
. 当直线 被圆
被圆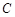 截得的弦长为
截得的弦长为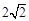 时, 求(1)
时, 求(1) 的值; (2)求过点
的值; (2)求过点 并与圆
并与圆 和点
和点 (1)若过点
(1)若过点 有且只有一条直线与圆
有且只有一条直线与圆 相切,求正实数
相切,求正实数 的值,并求出切线方程;(2)若
的值,并求出切线方程;(2)若 ,过点
,过点 互相垂直,设
互相垂直,设 分别为圆心到弦
分别为圆心到弦 的值;
的值; 的最大值.
的最大值.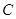 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆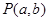 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,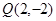 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为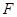 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点 的离心率为
的离心率为 ,其中左焦点
,其中左焦点 .
.  与曲线C交于不同的A、B两点,且线段AB的中点M在圆
与曲线C交于不同的A、B两点,且线段AB的中点M在圆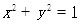 上,求m的值.
上,求m的值. 的圆的方程.
的圆的方程. 与
与 的交点,且圆心在直线
的交点,且圆心在直线 上的圆的方程.
上的圆的方程.