题目内容
7.已知等差数列{an}的首项为a,公差为d,且不等式ax2-3x+2<0的解集为(1,d).(1)求数列{an}的通项公式an;
(2)若bn=an($\frac{1}{2}$)${\;}^{{a}_{n}}$,数列{bn}前n项和Tn,证明$\frac{1}{2}$≤Tn$<\frac{10}{9}$.
分析 (1)显然x=1为方程ax2-3x+2=0的一个解,进而可知a=1、d=2,从而可得结论;
(2)通过an=2n-1可知bn=$\frac{2n-1}{{2}^{2n-1}}$,利用错位相减法可知Tn=$\frac{10}{9}$-$\frac{12n+10}{9}$•$\frac{1}{{4}^{n}}$,进而可得结论.
解答 (1)解:∵不等式ax2-3x+2<0的解集为(1,d),
∴a-3+2=0,即a=1,
∴x2-3x+2<0的解集为(1,2),即d=2,
∴数列{an}的通项an=1+2(n-1)=2n-1;
(2)证明:∵an=2n-1,
∴bn=an($\frac{1}{2}$)${\;}^{{a}_{n}}$=$\frac{2n-1}{{2}^{2n-1}}$,
∴Tn=1•$\frac{1}{2}$+3•$\frac{1}{{2}^{3}}$+5•$\frac{1}{{2}^{5}}$+…+(2n-1)•$\frac{1}{{2}^{2n-1}}$,
$\frac{1}{{2}^{2}}$•Tn=1•$\frac{1}{{2}^{3}}$+3•$\frac{1}{{2}^{5}}$+…+(2n-3)•$\frac{1}{{2}^{2n-1}}$+(2n-1)•$\frac{1}{{2}^{2n+1}}$,
两式相减得:$\frac{3}{4}$•Tn=$\frac{1}{2}$+2•($\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{5}}$+…+$\frac{1}{{2}^{2n-1}}$)-(2n-1)•$\frac{1}{{2}^{2n+1}}$
=$\frac{1}{2}$+2•$\frac{\frac{1}{{2}^{3}}(1-\frac{1}{{2}^{2n-2}})}{1-\frac{1}{{2}^{2}}}$-(2n-1)•$\frac{1}{{2}^{2n+1}}$
=$\frac{5}{6}$-$\frac{1}{3}•\frac{1}{{2}^{2n-2}}$-(2n-1)•$\frac{1}{{2}^{2n+1}}$
=$\frac{5}{6}$-$\frac{6n+5}{6}$•$\frac{1}{{4}^{n}}$,
∴Tn=$\frac{4}{3}$[$\frac{5}{6}$-$\frac{6n+5}{6}$•$\frac{1}{{4}^{n}}$]=$\frac{10}{9}$-$\frac{12n+10}{9}$•$\frac{1}{{4}^{n}}$,
∵对任意的正整数n$\frac{12n+10}{9}$•$\frac{1}{{4}^{n}}$>0恒成立,
∴Tn$<\frac{10}{9}$,
又∵Tn≥T1=b1=$\frac{1}{2}$,
∴$\frac{1}{2}$≤Tn$<\frac{10}{9}$.
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
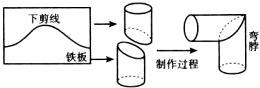 铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.
铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.