题目内容
【题目】已知函数![]() .
.
(I)求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(II)求证:当![]() 时,
时, 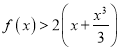 .
.
(III)设实数![]() 使得
使得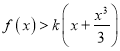 对
对![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)见解析;(III)
;(II)见解析;(III)![]() 最大值为
最大值为![]() .
.
【解析】试题分析:(I)![]() ,得
,得![]() ,又
,又![]() ,可得在
,可得在![]() 处切线方程为
处切线方程为![]() .
.
(II)令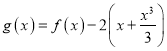 ,求导得出
,求导得出![]() 的增减性,然后由
的增减性,然后由![]() 得证.
得证.
(III)由(II)可知,当![]() 时,
时, 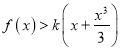 对
对![]() 恒成立.
恒成立. ![]() 时,令
时,令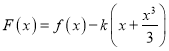 ,求导,可得
,求导,可得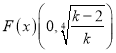 上
上![]() 单调递减,当
单调递减,当![]() 时,F
时,F![]() , 即当
, 即当![]() 时,
时, 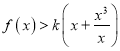 ,对
,对![]() 不恒成立,可得k的最大值为2.
不恒成立,可得k的最大值为2.
试题解析:(I)∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
, ![]() ,
,
∴在![]() 处切线方程为
处切线方程为![]() .
.
(II)证明:令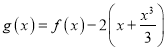 ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴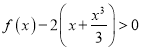 ,
,
即在![]() 时,
时, 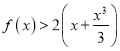 .
.
(III)由(II)知,在![]() 时,
时,
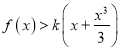 对
对![]() 恒成立,
恒成立,
当![]() 时,令
时,令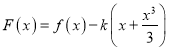 ,
,
则![]() ,
,
![]() ,
,
∴当![]() 时,
时, ![]() ,
,
此时在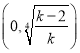 上
上![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,
,
即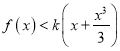 ,
,
∴当![]() 时,
时, 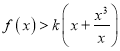 ,
,
对![]() 不恒成立,
不恒成立,
∴![]() 最大值为
最大值为![]() .
.
点晴:本题主要考查函数导数与不等式,恒成立问题.要证明一个不等式,我们可以先根据题意所给条件化简这个不等式,如第二问的不等式,可以转化为 ,第三问的不等式可以转化为
,第三问的不等式可以转化为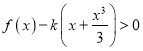 ,划归与转化之后,就可以假设相对应的函数,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.
,划归与转化之后,就可以假设相对应的函数,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.

练习册系列答案
相关题目