题目内容
如图,正三棱柱ABC-A'B'C'中,D是BC的中点,AA'=AB=2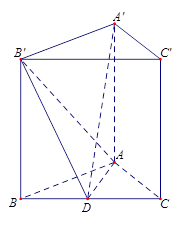
(1)求证:AD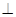 B'D;
B'D;
(2)求三棱锥A'-AB'D的体积。
(1)详见解析;(2)体积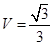 .
.
解析试题分析:(1)在立体几何中证明直线与平面垂直,一般有以下两种方法:一是通过线面垂直来证明;二是用勾股定理来证明.在本题中,证明哪条直线垂直哪个平面?在正三棱柱 中,因为
中,因为 为
为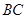 中点,所以
中点,所以 ,由此可得
,由此可得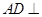 平面
平面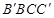 ,从而
,从而 .另外,求出
.另外,求出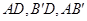 三边的长,用勾股定理也可证得.
三边的长,用勾股定理也可证得.
(2)求三棱锥的体积一定要注意顶点的选择.思路一、连结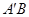 交
交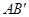 于点
于点 ,则
,则 为
为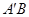 的中点,所以点
的中点,所以点 到平面
到平面 的距离等于点
的距离等于点 到平面
到平面 的距离,所以可转化为求三棱锥
的距离,所以可转化为求三棱锥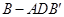 即三棱锥
即三棱锥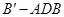 的体积,这样求就很简单了.思路二、转化为求三棱锥
的体积,这样求就很简单了.思路二、转化为求三棱锥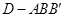 的体积.
的体积.
试题解析:(1)法一、在正三棱柱 中,平面
中,平面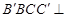 平面
平面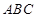 ,平面
,平面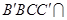 平面
平面 ,
,
又因为 ,
,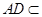 平面,所以
平面,所以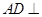 平面
平面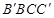 ,
,
又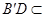 平面
平面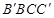 ,所以
,所以 . 6分
. 6分
法二、易得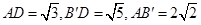 由勾股定理得
由勾股定理得 . 6分
. 6分
(2)法一、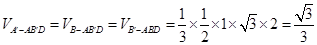 .
.
法二、 . 12分
. 12分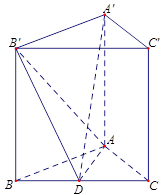
考点:1、直线与直线垂直的判定;2、三棱锥的体积.

练习册系列答案
相关题目
 为圆
为圆 的直径,点
的直径,点 .
.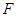 在圆
在圆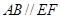 ,矩形
,矩形 所在的平面和圆
所在的平面和圆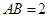 ,
,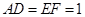 .
.
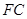 的中点为
的中点为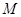 ,求证:
,求证: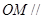 平面
平面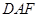 ;
;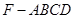 的体积.
的体积.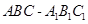 中,
中,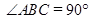 ,
, ,求:
,求: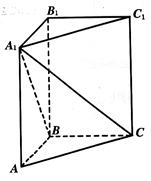
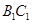 与
与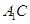 所成角的大小;
所成角的大小;  的体积.
的体积.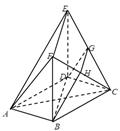
 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.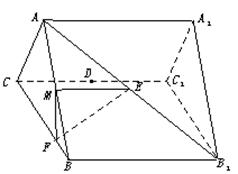
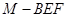 的体积.
的体积. 的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

 ;
; 与平面
与平面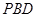 所成角的正弦值.
所成角的正弦值. 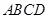 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面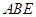 ,
, ,
, ,
,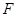 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE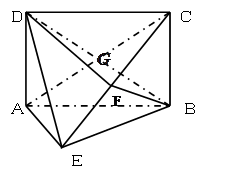
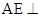 平面
平面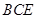 ;
;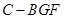 的体积.
的体积.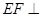 平面
平面 ,
, ,
,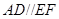 ,
,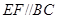 ,
,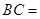
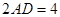 ,
,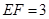 ,
,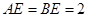 ,
,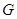 是
是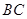 的中点.
的中点.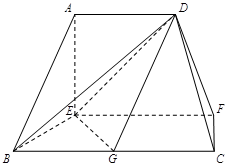
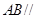 平面
平面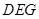 ;
;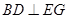 ;
;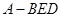 的体积.
的体积.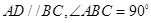 ,求图中阴影部分绕A
,求图中阴影部分绕A B旋转一周形成的几何体的表面积和体积.
B旋转一周形成的几何体的表面积和体积.